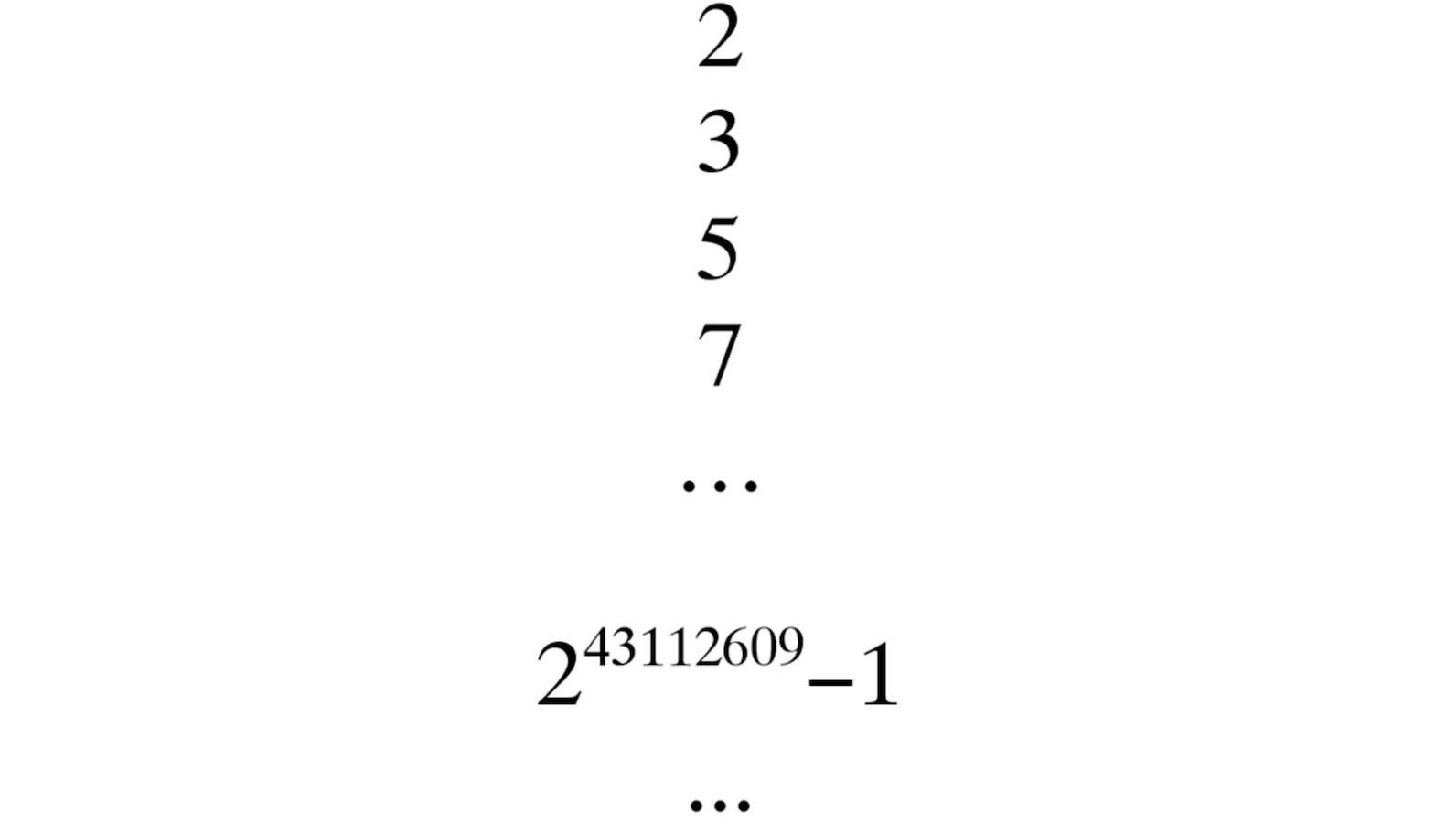
J’avais l’intention d’écrire un petit billet intitulé « Mathématiques financières et faux-monnayage » en réponse à l’article « La crise expliquée par les maths » du Monde, au titre délicieusement ambigu (et en particulier à la phrase « Cette situation de pénurie n’est pas prévue dans les modèles, qui considèrent que tout produit financier est à tout moment disponible sur le marché »), mais ce sera pour une autre fois (peut-être).
À la place, je vais parler de nombres premiers. Euler a démontré (en 1737) qu’il y a beaucoup de nombres premiers puisque la somme de leurs inverses vaut \(+\infty\).
Par comparaison, il y a peu de nombres dont l’écriture en base \(10\) ne comporte pas de \(9\) puisque la somme des inverses de ces nombres est finie (je présume que
Xenon aurait pu se persuader de la véracité de ce fait).
Une autre manière de faire la comparaison est de constater que jusqu’à \(10^n\), il y a seulement \(9^n\) nombres sans \(9\) dans l’écriture en base \(10\), ce qui fait une proportion de \((0,9)^n\), alors que la proportion de nombres premiers est de l’ordre de \(\frac{1}{n\log 10} \sim \frac{1}{2,3\,n}\), d’après le théorème des nombres premiers démontré par Hadamard et de la Vallée-Poussin (en 1896) après plus d’un siècle d’essais infructueux (par Euler, Gauss, Riemann, Tchebychev…).
Comme \((0,9)^n\) tend vers \(0\) beaucoup plus vite que \(\frac{1}{n}\), cela montre qu’il y a beaucoup plus de nombres premiers que de nombres sans \(9\).
Pourtant, une petite simulation en tirant des nombres au hasard vous prouvera qu’il y a beaucoup plus de nombres sans \(9\)
que de nombres premiers. Par ailleurs, on a distribué, il n’y a pas très longtemps, \(100\,000\) dollars à ceux qui ont découvert
le nombre premier \(2^{43\,112\,609}-1\), sous prétexte que ce nombre avait plus de \(10\) millions de chiffres, alors que je peux produire
sans aucun problème un nombre de un milliard de chiffres sans \(9\) (je réfléchirai à deux fois si on me demande de l’écrire
in extenso à la main…), ce qui ne me rapportera rien du tout. Alors, nous aurait-on menti ou y aurait-il d’autres manières de ranger les nombres que par
leur taille?
ÉCRIT PAR
Pierre Colmez
Directeur de recherche - CNRS - Sorbonne Université, Paris
22h24
du 9, pour créer un monde neuf !
Alors qu’on put produire un roman sans « e » ([1]), que dire des mathématiques « sans 9 » ?
Pour commencer : que sait-on des nombres premiers « sans 9 » ? Et enfin, combien de 9 dans l’écriture en base 10 de \(2^4 3112609−1 \)? Est-ce en particulier un nombre premier de « l’ancien monde », ayant le chiffre 9 dans son écriture décimale ?
Enfin, sérieux problème : comment faire une preuve par …, euh …, par 9 ! ([2]) dans ce nouveau monde ?
[1] G. Perec, « La disparition ». Denoël, 1969
[2] Comment cela, pas encore de billet là-dessus sur ce site ?