Un entrefilet du Cactus de l’Humanité du Jeudi…

Un message électronique de Jean-Pierre Kahane présentant un projet de billet

Un entrefilet du Cactus de l’Humanité du Jeudi 29 mars nous apprend que le parti intitulé la « Gauche moderne » a apporté son soutien à Nicolas Sarkozy par un vote massif, à savoir par 76,29 % des délégués et ajoute « Mystère : le communiqué n’indique pas sur quel nombre de « délégués » porte ce pourcentage… ». En vérité, dans sa précision ridicule, la donnée fournit une réponse : le nombre de votants était 97 ou un multiple de 97, et le vote a été acquis par 74 voix sur 97, ou 148 voix sur 194 etc. Je penche pour 74/97, parce que les rédacteurs du communiqué ont dû vouloir compenser le dérisoire du nombre par le gonflement de l’écriture décimale.

Question. Comment ai-je trouvé 74/97 ?

C’est la meilleure approximation de 0,7629 par une fraction raisonnable, et je l’ai calculée au lit cette nuit avec une calculette par un procédé très connu qui est celui des fractions continuées : je prends l’inverse, j’en extrais la partie entière et je prends l’inverse de la partie décimale, et je continue jusqu’à ce que la fraction obtenue soit suffisamment proche de 0,7629.

Cela donne :

\(1/0,7629 \simeq 1 + 0,310787783\)

\(1/0,310787783 \simeq 3+0,217629697\)

\(1/0,217629697 \simeq 4+ 0,594961137\)

\(1/0,594961137 \simeq 1+0,680782051\)

\(1/0,680782051 \simeq 1+0,468898891\)

\(1/0,468898891 \simeq 2 + 0,132655929\)

si bien que

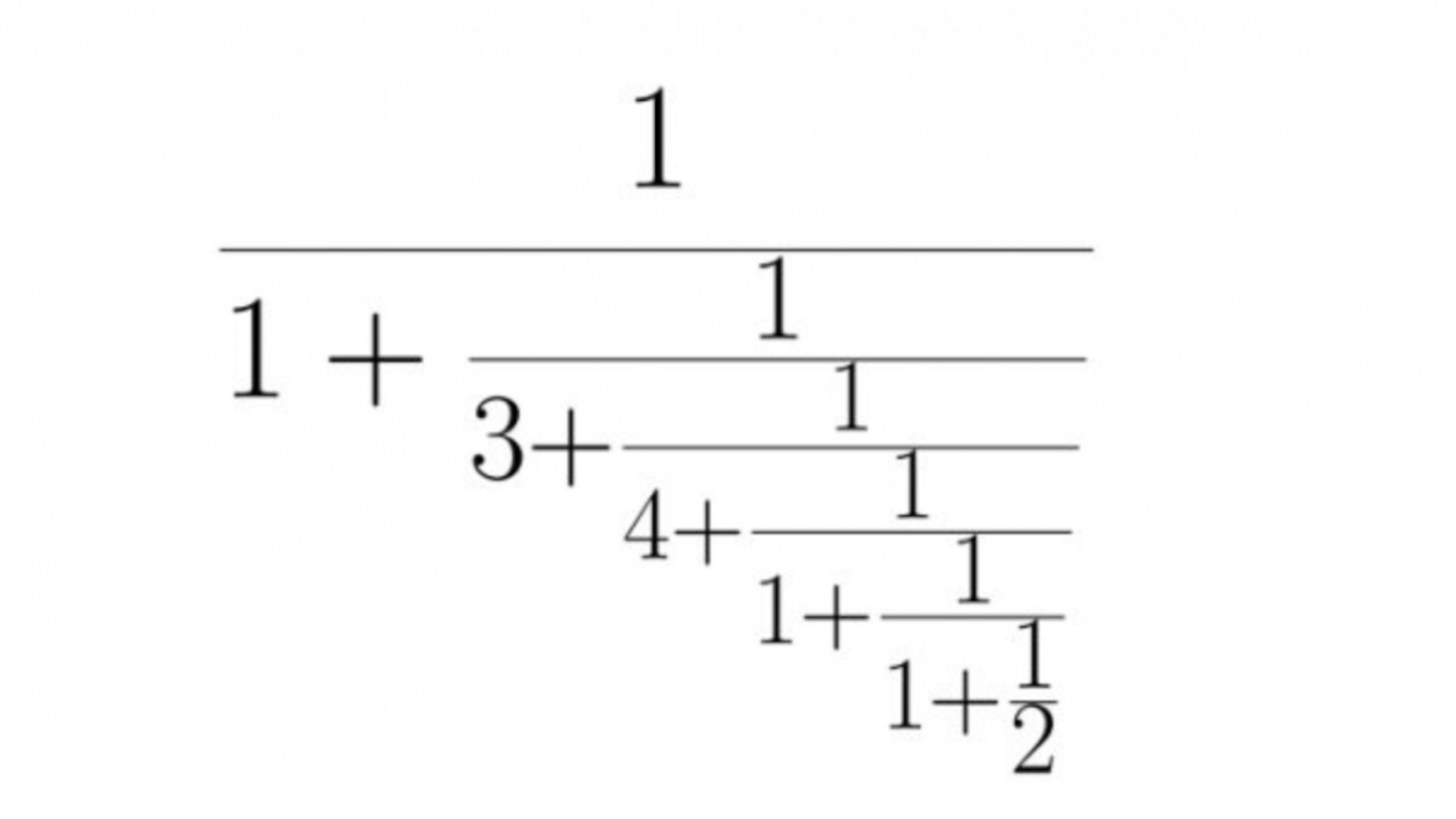
\({\large
0,7629 \simeq } {\Huge \frac{1}{1+\frac{1}{3+\frac{1}{4+\frac{1}{1+\frac{1}{1+\frac{1}{2}}}}}}
}\)

et cette dernière fraction continuée est égale à \(\frac{74}{97}\) et ne diffère de 0,7629 que d’environ 0,000013.

 

Leçons

• On peut tirer de données numériques plus qu’elles ne croient fournir.

• L’Humanité a bien fait d’épingler le ridicule de cette expression chiffrée.

• Si ce billet est publié, il montrera au lecteur un modeste usage des fractions continuées, un procédé mathématique très ancien et très actuel aussi.

Une réponse d’Étienne Ghys

Peut-être que tu as toujours une calculette à côté de toi, mais moi j’ai toujours Maple à proximité ! Je joins ce que Maple me répond lorsque je lui demande de développer 7629/10000 en fractions continues.

.

On a donc les approximations 74/97, 547/717, 621/814, 1168/1521, et évidemment 7629/10000.

Je me demande cependant en quoi ces fractions continues répondent à la question posée ? S’il y a eu \(q\) votants dont \(p\) pour Sarkozy, on sait que \(0,7629\) est «le nombre décimal à quatre chiffres après la virgule» qui approche le mieux \(p/q\). Autrement dit :

\(\vert \frac{p}{q} – \frac{7629}{10000} \vert <0,00005 \)

et la question est donc de savoir quelles sont les valeurs de \(q\) pour lesquelles il existe une valeur de \(p\) qui vérifie cette inégalité.

Evidemment ta solution \(q= 97\) est bonne, de même que les dénominateurs suivants 717, 814, 1521, et évidemment 10000. Mais on peut aussi demander à Maple d’en chercher d’autres. Si on cherche les solutions inférieures à 500, on trouve 97, 194, 232, 291, 329, 350, 367, 388, 426, 447, 464, 485.

194 n’est pas une surprise puisque c’est le double de 97 mais 232 n’apparaît pas dans la fraction continue. Il pourrait très bien y avoir eu 232 votants, par exemple ? Il y aurait alors eu 177 partisans de N. Sarkozy et 177/232 vaut en effet à peu près 0,7629310345, c’est-à-dire environ 76,29% si on s’en tient à deux décimales pour le pourcentage.

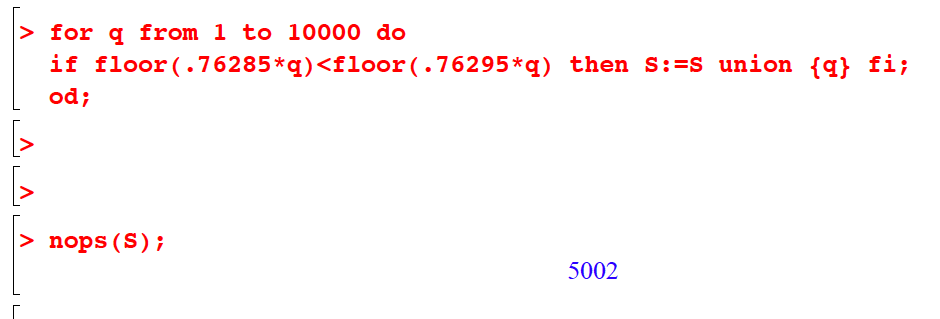
Bien entendu tous les entiers supérieurs à 10000 sont des solutions à notre problème. Maple trouve 5002 solutions inférieures à 10000 ³On laisse le lecteur réfléchir à la question de savoir s’il est étonnant que le nombre de solutions soit de l’ordre de la moitié de 10000.

.

L’ensemble des entiers \(q\) qui sont solutions de notre problème est un semi-groupe : la somme \(q_1+q_2\) de deux solutions \(q_1,q_2\) en est encore une. C’est clair puisque si \(p_1,p_2,q_1,q_2\) sont des entiers naturels, le rationnel \(\frac{p_1+p_2}{q_1+q_2}\) est compris entre \(\frac{p_1}{q_1}\) et \(\frac{p_2}{q_2}\).

La structure des semi-groupes d’entiers naturels non nuls est un sujet d’étude contemporain. Voici cependant une chose facile concernant ces semi-groupes. Tout semi-groupe contient un nombre fini d’éléments qui ne sont pas la somme de deux éléments du semi-groupe et qu’on peut qualifier d’indécomposables. Alors, tout élément du semi-groupe peut s’écrire comme une somme d’éléments indécomposables.

Dans le cas qui nous intéresse, (Maple montre qu’) il y a 10 éléments indécomposables ⁴Merci à Shalom Eliahou qui m’a expliqué que mon premier calcul était faux…, à savoir :

97, 232, 350, 367, 502, 603, 856, 1139, 2821, 7607.

La seule chose qu’on peut donc conclure c’est que le nombre de votants de la « Gauche moderne » est une somme d’un certain nombre de ces dix entiers, en s’autorisant d’ailleurs à utiliser plusieurs fois le même !

A mon avis, ce sont ces dix entiers qu’il faut considérer plutôt que les fractions continues.

On apprend sur le site web de ces braves gens que « La Convention Nationale de La Gauche Moderne s’est tenue à Paris ce samedi 24 mars en présence de très nombreux délégués venus de toute la France, métropolitaine et de l’Outre-Mer ». La photo suivante, extraite de ce site, nous ramène heureusement à la réalité et montre même que ton estimation de 97 votants paraît excessive !

.

Amitiés,

Étienne