Un roman dont l’héroïne est une formule

 

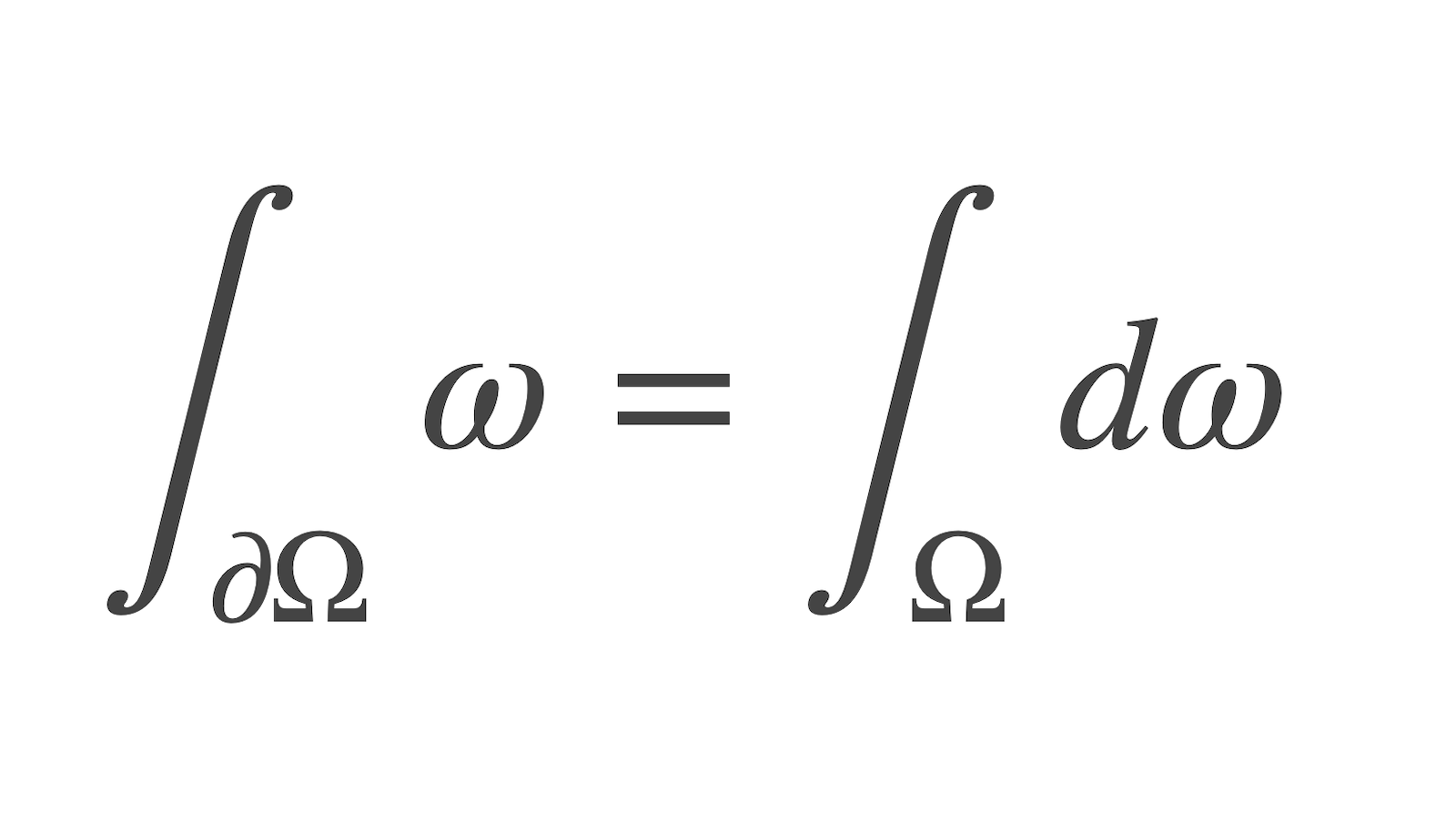
Il n’est pas si fréquent de lire des romans mathématiques. Il est encore plus rare de lire des romans mathématiques dont le héros est une héroïne. Il est donc tout à fait improbable de se retrouver à lire un roman mathématique dont l’héroïne est une formule.

1er avril : Dans Balade parmi les aires et les volumes, on apprend que le principe de Cavalieri dit que si on découpe deux solides de même hauteur en tranches horizontales et que, à même hauteur, deux tranches ont toujours même aire, alors les deux solides ont même volume. Et comme application de ce principe, une jolie formule, le volume \(V\) de la boule de rayon \(R\) :
\[ V = \frac{4}{3}\pi R^3.\]

30 juin : Il est question dans ce billet d’ésthétique en mathématique, d’une formule que l’on peut trouver belle sans toutefois comprendre sa signification précise. Cette formule exprime un théorème qui a un nom, peut-être même plusieurs d’ailleurs, signe sans doute d’une jeunesse tourmentée et riche. Traversant les années, les pays et de nombreuses péripéties, cette formule a atteint l’âge de maturité et une formulation particulièrement élégante qui nous fait oublier toutes les mathématiques qu’il a fallu défricher pour arriver là.

17 juillet : La formule préférée du professeur. Tiens, un roman mathématique. Le héros est un théoricien des nombres mais n’est pas un génie qui calcule et démontre des théorèmes incroyables à longueur de journée avec suffisamment de temps libre de surcroît pour se permettre de faire le boulot de trois agents du FBI à lui tout seul. Un mathématicien ordinaire peut-être ?

2 août : Dans Weil, Cartan, la prison et l’intégrale, on apprend l’existence d’une chemise dans les archives de l’Académie des sciences avec écrite dessus : « Manuscrit d’André Weil, écrit en prison en 1940 à l’intention de Bourbaki (c’est le seul manuscrit connu d’André Weil, qui n’écrivait qu’avec sa machine à écrire). Don d’Henri Cartan, 28 mars 1994 ». Ce manuscrit permet de comprendre comment Weil concevait l’exposé de la théorie de l’intégration, avec une axiomatique simple des fonctions à intégrer et le fait que le langage des probabilités devait être introduit dès le premier paragraphe.

6 novembre : « S’il-vous-plaît, qu’est-ce que c’est qu’une variété ? » Considérez l’ensemble des droites dans le plan. C’est bien plus qu’un ensemble, c’est justement une variété. Exercice : reconnaître cette variété.

28 novembre : Variétés, sous-variétés, orientation, bord, homologie, nombres de Betti, dualité de Poincaré ! Dans son travail sur Analysis situs, Poincaré a été amené à définir avec précision l’intégrale sur une variété orientée d’une forme différentielle. « Je vais définir l’intégrale suivante

\[\int \sum X_{\alpha_1 \alpha_2 \cdots \alpha_m} \text{d}x_{\alpha_1}\text{d}x_{\alpha_2}\cdots\text{d}x_{\alpha_m}\]
[…] ». Du coup, il aurait pu l’écrire. Mais il ne l’a pas fait. La formule de Stokes.