A mi-chemin entre Bonn et Berlin, Göttingen est une charmante ville de Basse-Saxe, comptant surtout l’une des plus célèbres universités d’Allemagne : pas moins de 42 prix Nobel y ont étudié ou enseigné !
.
On peut lire les noms de très grands scientifiques un peu partout dans la ville : nom de rue bien sûr, petite plaque sur un mur pour indiquer une ancienne maison ou l’appartement de l’étudiant Riemann par exemple, établissement scolaire
.
et même bistrot !
.
Avec en fond musical la célèbre chanson de Barbara, quoi de plus beau cadre que le pays de Gauss pour une école d’été ?
Cette école a eu lieu la semaine dernière sous les regards vigilants de Gauss et Weber. Pour la petite histoire, lorsqu’un étudiant obtient son diplôme de doctorat, traditionnellement il doit grimper s’asseoir sur les genoux de Gauss
.
et offrir un baiser à Gänseliesel, la jeune gardienne d’oies (ce qui en fait la jeune femme la plus embrassée du pays !).
.
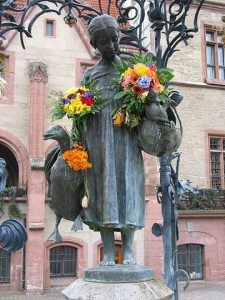
Pour cette école d’été, quatre maîtres de cérémonie pour quatre mini-cours passionnants autour de la théorie ergodique. Nous étions une trentaine (dont une vingtaine d’étudiants) et c’est dans une ambiance excellente que nous avons pu discuter de systèmes dynamiques mesurés, d’algèbres de von Neumann et de théorie géométrique des groupes : 4h de cours par jour, entrecoupés de discussions afin d’alimenter la séance de questions/exercices qui venaient clôturer chaque fin d’après-midi.
La théorie ergodique est probablement née dans les années 1871 lorsque Bolztmann travaillait à la théorie cinétique des gaz. Comme bien souvent, les mathématiciens se sont progressivement emparés de ce concept devenu central dans l’étude des systèmes dynamiques préservant une mesure. Commençons par un exemple simple : les translations sur la droite réelle. Il est intuitivement clair que si on considère un intervalle de \(\mathbf{R}\), disons \([-1,1]\) de longueur 2, et qu’on le translate par un nombre réel, par exemple \(\pi\), on obtient le nouvel intervalle \([\pi-1,\pi+1]\), toujours de longueur 2. Ainsi les translations préservent les longueurs des intervalles et si on s’amuse à itérer cette translation par \(\pi\), l’intervalle initial \([-1,1]\) va se déplacer progressivement sur la droite réelle mais sa longueur restera quant à elle échangée : c’est un premier exemple de système dynamique préservant une mesure, ici la longueur des intervalles.
Intéressons-nous maintenant au cercle de rayon 1 dans le plan euclidien et à une rotation d’angle \(\alpha\) sur ce cercle : c’est un autre exemple de système dynamique préservant une mesure (en fait, il ressemble beaucoup au précédent). Là encore, si on prend un petit intervalle sur le cercle et qu’on lui fait subir des rotations successives, sa longueur ne changera pas au cours du temps. Plus intéressant encore, selon la valeur de \(\alpha\), il se passe toujours l’un des deux phénomènes suivants :
– si \(\alpha/\pi\) est un nombre rationnel ( i.e. de la forme \(p/q\)), alors après un nombre fini d’itérations, n’importe quel point du cercle revient sur lui-même : il s’agit d’un système dynamique périodique ;
– si \(\alpha/\pi\) est un nombre irrationnel, alors aucun point du cercle n’est périodique. Plus intéressant encore, n’importe quel point du cercle a en fait tendance à se répartir tout autour du cercle, c’est-à-dire aussi proche que l’on veut de n’importe quel autre point de son choix.
La première situation est relativement simple à comprendre ; la deuxième est quant à elle beaucoup plus intéressante : c’est un prototype de système dynamique {ergodique} et il en existe bien entendu de très nombreux exemples, souvent extrêmement difficiles à analyser.
.
ÉCRIT PAR
Aurélien Alvarez
Professeur - Rédacteur en chef d'IdM - École normale supérieure de Lyon
8h55
Bonjour Monsieur Alvarez
J’aime beaucoup votre article avec ses belles photos.
Je crois que j’ai compris ce que vous dites avec les intervalle. J’ai un peu plus de mal avec le cercle : je ne comprends pas ce que représente la dernière photo.
Respectueusement
Ludmila
PS. Une petite question : comment font les femmes qui passent une thèse à Göttingen ? Elles embrassent aussi la gardeuse d’oie ? ou il y a aussi une statue de gardien de cochons sur une autre place ?
10h08
Chère Ludmila,
Merci pour votre message. J’essaie d’expliquer un peu mieux la fin de mon billet : prenons l’exemple d’une rotation R d’angle π/6 et fixons un point de départ quelconque P sur le cercle. Quand on itère la rotation, on voit apparaître les points P, R(P), R(R(P)), etc. Et au bout de 12 (=6*2) itérations successives, on retombe sur le point P : le système est périodique. Mais en fait, ceci marche encore si on change π/6 en π/q, où q est un nombre rationnel (non nul bien sûr).
Par contre, si q n’est plus un nombre rationnel (par exemple q=π), alors plus aucune trajectoire (suite d’itérations successives), n’est périodique. Et tout est plus compliqué du coup. Ainsi on va abandonner l’idée de vouloir comprendre toutes les trajectoires très précisément et on va plutôt essayer de comprendre les choses « en moyenne », une sorte d’étude statistique des trajectoires. Par exemple, on sait que les trajectoires passent un peu partout mais peut-on quantifier un peu ça ? Repassent-elles plus souvent encore à certains endroits que d’autres ? Et d’autres questions encore : c’est ça l’idée de la théorie ergodique. L’image que j’ai mise à la fin n’a rien à voir avec mon exemple des rotations : c’était juste pour illustrer des trajectoires compliquées qui s’emmêlent les unes dans les autres, bref l’idée qu’on a derrière la tête quand on pense au mot ergodique.
En espérant que ce soit un peu plus clair maintenant.
Aurélien.
PS : je crains que la tradition d’embrasser Gänseliesel remonte à une époque où le doctorat ne s’adressait pas aux femmes… et je n’ai pas entendu parler de gardien de cochons pour compenser ! Je dirais que les jeunes femmes docteurs font comme les garçons aujourd’hui, ou au moins lui offrent un bouquet de fleurs car Gänseliesel a toute l’année les bras bien chargés.
15h24
Chère Ludmila, cher Aurélien,
Permettez-moi d’ajouter mon grain de sel à vos post-scriptums (mais je ne trancherai pas la question de Gänseliesel et du porcher…).
Göttingen a été (avant la période nazie, ça va sans dire, mais disons-le quand même) un des lieux universitaires les plus libéraux et avancés d’Allemagne, et plusieurs femmes y ont passé des thèses de doctorat dans des disciplines scientifiques, dont voici quelques-unes :
dès le XVIIIe siècle (mais rappelons que l’université a été fondée en 1737), une certaine Dorothea Schözer Rhode y avait obtenu un diplôme
dans la première moitié du XIXe siècle, Gauss avait obtenu que l’université décernât un doctorat honorifique à Sophie Germain, qui malheureusement mourut (en 1831) avant de pouvoir le recevoir
en 1874, Sofia Kovalevskaya y obtenait son doctorat de mathématiques dans cette université (la soutenance eut lieu in absentia) [1]
la même année, une des amies de Sofia Kovalevskaya, Julia Lermontova, y soutint une thèse de chimie, après une soutenance « régulière »
la première thèse soutenue de façon « régulière » en mathématiques par une femme dans cette université l’a été par la mathématicienne anglais Grace Chisholm Young, sous la direction de Felix Klein, en 1895
(et, non, Emmy Noether n’y a pas passé la sienne, c’était à Erlangen !)
Bien à vous
[1] Elle étudiait avec Weierstrass à Berlin et c’est précisément à cause de la réputation de libéralisme de Göttingen que Weierstrass avait proposé sa thèse à cette université. Je vous renvoie à son portrait et aux références qu’il contient.