Il y a des poètes que j’aime relire, car ils me donnent de l’énergie, ils libèrent mon imagination, ils m’enthousiasment. Il y a de même des mathématiciens aux écrits desquels je reviens de temps en temps pour les mêmes raisons. Et je lis un peu au hasard leurs écrits, comme je ferais avec ceux des poètes qui me sont chers, car je sais qu’un peu tout me parle chez eux. Je les parcours comme je parcours les villes que j’aime, en me laissant attirer par une lumière sur une branche bourgeonnante au détour d’une rue.
L’un de ces mathématiciens est Hermann Weyl. C’est l’un des premiers mathématiciens à avoir réfléchi en profondeur aux conséquences mathématiques et philosophiques de la théorie de la relativité générale, puis de la mécanique quantique, et ceci dès leur bourgeonnement. Il y a réfléchi non pas seulement en technicien brillant, mais en penseur au sens antique du mot, soucieux de comprendre ce qui avait changé pour la pensée en général. Il fit de grands efforts pour expliquer cela à divers niveaux de sophistication. Dans cette démarche, il excellait à faire saisir des concepts subtils grâce à des analogies lumineuses. Je me souviens encore du bonheur que j’ai ressenti lorsque, il y a presque 15 ans, en début de thèse, je suis tombé sur l’analogie suivante qu’il voyait entre, d’une part, une particule soumise à un champ électrique et, d’autre part, un observateur regardant un objet :
Ici nous commençons avec la force comme étant l’objet donné ; mais les faits ébauchés nous mènent à concevoir un champ électrique, décrit mathématiquement par la fonction vectorielle E(P), qui entoure les conducteurs et qui existe, indépendamment du fait que la force exercée sur une particule test est constatée ou pas. La particule test sert seulement à rendre le champ accessible à l’observation et à la mesure. L’analogie complète avec le cas de la perspective est évidente. Le champ E d’ici correspond à l’objet là-bas, la particule test à l’observateur, sa charge à sa position ; la force exercée par le champ sur la particule test et changeant selon la charge de la particule correspond à l’aspect bidimensionnel offert par l’objet solide à l’observateur et dépendant du point de vue de celui-ci.
Ce texte se trouve à la page 114 d’un livre qui m’a beaucoup plu, « Philosophy of Mathematics and Natural Science », publié en 1949 par Princeton University Press. Le contexte de l’extrait ci-dessus est celui de l’explication de la manière dont s’est forgé un objet fondamental de la physique du XIX-ème siècle, le concept de champ électrique. J’avais suivi des cours à ce sujet en classes préparatoires, très mathématisés. Par ailleurs j’avais appris un peu de géométrie projective et j’avais rêvé à sa lointaine origine dans les ateliers des artistes du Quattrocento. La brusque mise en contact de ces deux mondes a créé en moi un frisson de joie dont je me souviens encore comme de l’une des plus claires manifestations du plaisir poétique que j’ai ressentie en mathématiques.
Depuis, l’une de mes principales obsessions lorsque j’enseigne est de faire percevoir puis développer de belles analogies. Un avantage immédiat est une économie de pensée, tout ce qui a été compris d’un côté servant soudain de guide à la compréhension de l’autre. Un avantage indirect est que cela habitue à ressentir soit la cohérence du monde, soit celle de notre manière de le regarder, ce qui permet de lutter contre la perte de vision globale causée par le brouillard dont les particules sont une multitude de langages hyperspécialisés.
Mais saisir des analogies est aussi très important lors du processus de recherche. Car les analogies peuvent être le signe de liens profonds entre deux structures du monde. Une fois une analogie découverte, cela peut être le travail de plusieurs générations de dévoiler ses ramifications. J’espère que sur ce site apparaîtront de temps en temps des récits de telles grandes analogies ayant nourri le développement scientifique.
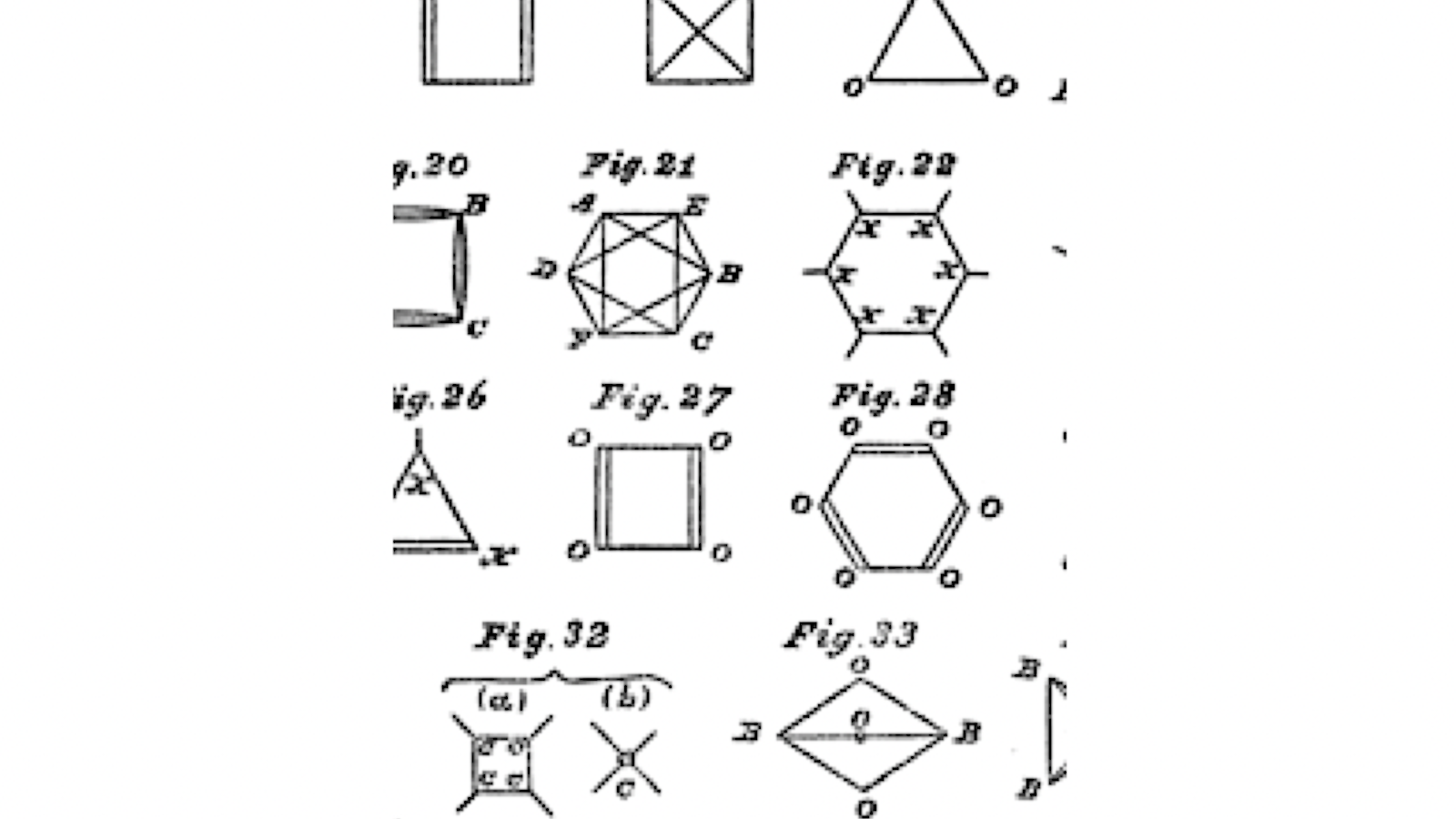
Mais comment découvre-t-on des analogies ? Cela est assez mystérieux : après un processus de maturation inconscient, elles surgissent brusquement dans la conscience. Il y a un texte fameux d’Henri Poincaré concernant une telle naissance brutale, lors de la montée dans un omnibus à Coutances 2On pourra lire cet épisode dans le texte de Poincaré, « L’invention mathématique 1 » (in L’Enseignement Mathématique, Volume 10, 1908), disponible ici sur la page du SEALS en Suisse, et d’où provient l’extrait suivant.
. Mais, dans le même livre que précédemment, à la page 273, on trouve un autre exemple, moins connu. Hermann Weyl cite l’introduction d’un article publié en 1878 par James Joseph Sylvester dans l’American Journal of Mathematics. Sylvester y explique comment, inspiré par les diagrammes introduits par le chimiste Kekulé pour représenter les molécules composées – et qui sont depuis la base graphique de la chimie organique – il a découvert une méthode graphique dans une branche des mathématiques pures dont il était l’un des principaux spécialistes mondiaux, la théorie des invariants :
Pendant une nuit où j’étais étendu dans mon lit, en cherchant à découvrir un moyen de transmettre une conception intelligible des objets de l’algèbre moderne à une société mixte principalement composée de physiciens, chimistes et biologistes, entremêlée de quelques rares mathématiciens […] impressionné depuis longtemps par le sentiment d’affinité, sinon d’identité d’objet entre la recherche sur les radicaux composés et la recherche des `Grundformen’ ou des invariants irréductibles, j’ai été agréablement surpris de découvrir soudain représentée sur ma rétine mentale une image chimico-graphique servant à incarner et illustrer les relations de ces formes algébriques dérivées avec leurs primitives et avec leurs semblables, ce qui allait parfaitement accomplir l’objet que j’avais en vue, comme je vais l’expliquer maintenant.
On trouvera l’article de Sylvester numérisé sur le site de l’Université de Michigan, à partir de la page 148 (cf. le fichier PDF suivant (2Mo), mis à disposition sur cette page).
Ce que l’on apprend en lisant le livre de Hermann Weyl est que cette analogie découverte par Sylvester était en fait le signe d’un lien profond entre théorie des invariants et structures moléculaires. Mais ce lien n’allait être mis en évidence qu’une soixantaine d’années plus tard, après l’avènement de la mécanique quantique. Hélas, les explications de Hermann Weyl ne peuvent être suivies que par une personne ayant une formation mathématique supérieure poussée. Mais ce serait un défi extrêmement intéressant à relever que d’essayer d’expliquer cela à un public plus large sur ce site ! Peut-être, tel Sylvester, celui s’adonnant à cette tâche découvrira-t-il de nouvelles analogies fructueuses ?
ÉCRIT PAR
Patrick Popescu-Pampu
Professeur - Université de Lille
