
À tous nos lectrices et lecteurs, nous vous prions d’excuser le retard de la publication de la revue de presse de ce mois de novembre. En raison de plusieurs indisponibilités, une version réduite de notre équipe s’est chargée de vous concocter cette revue de presse, expliquant son retard et sa taille réduite. Nous profitons pour vous indiquer que si vous appréciez la lecture de nos revues de presse et que vous avez envie de participer à sa rédaction, vous êtes le/la bienvenue dans notre super équipe 🙂
Au programme de ce mois-ci, retrouvez : des réformes changeantes de l’éducation nationale, les lauréats et lauréates du Collège de France, des contre-exemples ou des conseils lectures qui vous donneront des envies de cadeaux.
Le 21 novembre, la neige a surpris une grande partie de la France par son intensité et sa tenue au sol. Nous ne résistons pas à sauter sur l’occasion pour afficher en image de Une une jolie photographie de flocons de neige prise par le photographe américain, Wilson Alwyn Bentley. Il est le premier à avoir réalisé des prises de vue de ces cristaux de glaces.
Bonne lecture et au nom de toute l’équipe : Bonnes fêtes de fin d’année !
À la une
Saluons une jolie manière de diffuser les travaux de recherche des doctorants et doctorantes. Après le concours Sciences en bulles ou Ma thèse en 180 secondes, voici Ma Thèse en Manga. “Nous cherchions alors à valoriser les travaux des doctorants et jeunes docteurs, et je me suis dit que le manga serait un support idéal. Ce média est en effet plébiscité par les adolescents et par le grand public : il représente un livre sur sept vendu en France et 26 % du chiffre d’affaires du secteur de l’édition. Le manga est aussi un format plus facile d’accès face aux problématiques d’illettrisme, d’accès à la lecture et de décrochage scolaire que l’on rencontre en Outre-Mer et en zones prioritaires”, explique celui qui pilote cette initiative : Dimitri Béchacq, chargé de recherche CNRS au laboratoire Pouvoirs, Histoire, Esclavages, Environnement Atlantique Caraïbe.
Cette initiative nous vient tout droit de la Martinique, où elle a été mise en place cette année. Les doctorants et doctorantes qui souhaitent participer doivent rédiger une lettre de motivation dans laquelle ils décrivent la manière dont ils aimeraient que leurs travaux soient partagés dans le manga. Les deux lauréats ont ensuite élaboré avec l’illustrateur, Raphaël « Raphy » Décilap, deux mangas de 28 pages : « Histoire de Louis » traite de l’homosexualité en Haïti et est transposée des travaux de thèse de Carlo Handy Charles ; « Nouveaux récits sur l’esclavage », est quant à lui issu de la thèse de Jessica Balguy.
Recherche et applications
Qu’est-ce qui rend le nombre 13 532 385 396 179 “vraiment spécial” ? MeteoGiornal l’explique dans un article.
Mais pour cela, un détour par le nombre 60 s’impose. Si on le décompose en facteurs premiers, on obtient 60=2²×3×5. Conservons tous les chiffres de cette décomposition dans leur ordre d’apparition (facteurs premiers et puissances) pour constituer le nombre 2 235. À nouveau, on le découpe en facteurs premiers 2 235=3×5×149 et on colle les facteurs premiers (il n’y a pas de puissances supérieures ou égales à 2) pour faire un nouveau nombre. Le nombre 35 149 ainsi obtenu est premier.

John Conway
Or il était conjecturé, notamment par John H. Conway, que peu importe le nombre choisi au départ, cette méthode conduit au final sur un nombre premier. C’était conjecturé, jusqu’à ce qu’on s’intéresse à 13 532 385 396 179. Car c’est un contre-exemple. Que se passe-t-il pour lui ? On a cette décomposition :
13 532 385 396 179=13×53²×3 853×96 179. Et si on crée un nouveau nombre en suivant la règle ci-dessus on obtient 13 532 385 396 179 – le nombre de départ. Le voilà notre contre-exemple.
L’article de journal italien est basé sur une vidéo de 2017 de la chaîne de vulgarisation mathématique Numberphile (en anglais).
Le singe savant n’aura jamais assez de temps
Un des paradoxes les plus connus des mathématiques est celui “du singe savant“. Celui-ci dit qu’un singe qui taperait au hasard sur une machine à écrire pendant un temps infiniment long tapera n’importe quel texte presque sûrement à un moment donné, l’entière œuvre de Shakespeare par exemple.
Mais voilà, que se passe-t-il si on ne laisse le singe (ou une armée de 200 000 singes) devant la machine que pendant un temps très long ? Deux chercheurs australiens, Jay Falletta et Stephen Woodcock, se sont amusés à faire les calculs.

Selon eux, la probabilité que le singe – et plus précisément un chimpanzé – tape tout Shakespeare pendant sa vie n’est que de \(10^{-7 448 357}\). Disons donc hautement improbable. Et si on imagine 200 000 chimpanzés en train de taper pendant \(10^{100}\) années, c’est toujours très très improbable. Avec une probabilité d’environ \(6,4×10^{-7 448 254}\) que cela se réalise.
L’article de recherche a été publié dans Franklin Open à la fin octobre et fut repris dans plusieurs médias comme NewScientist (en anglais), Sciences et Avenir ou ActuaLitté.
La conjecture des lits superposés est fausse !
Et le magazine anglophone Quantamagazine explique ce résultat récemment établi (mais pas encore validé par les pairs) par Nikita Gladkov, Igor Pak, tous deux de l’Université de Californie à Los Angeles, et Aleksandr Zimin, du MIT.
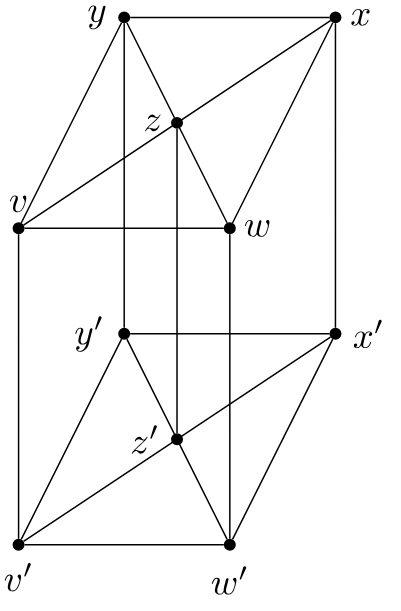
Exemple d’un graphe en lit superposé
Cette conjecture (appelée Bunkbed conjecture en anglais) parle d’un type de graphes particuliers, ceux qui ressemblent à des lits superposés. Expliquons, ils sont faits de deux parties identiques (les lits) reliées entre elles (un peu comme les longues tiges métalliques entre les lits).
À chacun des nœuds du graphe est associée une probabilité, mais qui respecte une règle : aux mêmes parties des lits (par exemple w et w’) est attribuée la même probabilité.
Maintenant, construisons un autre graphe qui sera le même que notre premier, mais sur lequel certaines arêtes vont disparaître de manière aléatoire selon la probabilité qui leur était associée.
La conjecture disait : “la probabilité qu’un sommet x dans la couchette supérieure soit connecté à un sommet y dans la couchette supérieure est supérieure ou égale à la probabilité que x soit connecté à y′.”
Mais les trois chercheurs ont trouvé un contre-exemple !
L’IA s’intéresse aux mathématiques
Pour mesurer les performances des modèles d’intelligence artificielle, il faut des benchmarks, des repères pour mesurer leurs performances. Par exemple, il existe des bases de données d’images qui permettent d’évaluer la performance d’un modèle sur la reconnaissance d’objets, d’animaux, de lettres.
Un nouveau type de benchmark vient d’être mis au jour, fait de problèmes de mathématiques. Dans IT for Business, Laurent Delattre présente FrontierMath : “une collection de centaines de problèmes mathématiques originaux et inédits. Ces problèmes, élaborés en collaboration avec plus de 60 mathématiciens de renom, couvrent un large éventail de domaines, allant de la théorie des nombres à la géométrie algébrique. Contrairement aux benchmarks existants comme GSM-8K ou MATH, qui sont désormais bien maîtrisés par les modèles d’IA actuels, FrontierMath offre un niveau de difficulté sans précédent qui promet de sérieusement challenger les IA à venir dans les prochaines années.”
Ce benchmark répond à une limitation des systèmes actuels : la réflexion. “Si l’intelligence artificielle (IA) a fait des progrès remarquables dans de nombreux domaines, de la compréhension du langage à la génération de texte en passant par la reconnaissance d’images, force est de reconnaître qu’elle pèche encore dans d’autres domaines privilégiant une réflexion approfondie […] Pour nombre d’experts, il est l’heure de relever la barre et de soumettre aux futures IA de 2025 des tests plus avancés réclamant des raisonnements plus élaborés.” Preuve de la difficulté des problèmes, GPT-4o et Gemini 1.5 Pro échouent sur 98 % des questions.
Ainsi, FrontierMath permettra de mesurer les performances des IA sur les raisonnements complexes. “En proposant des problèmes “à l’épreuve des devinettes”, où une solution correcte ne peut être obtenue que par un raisonnement approfondi, ce benchmark garantit que les IA ne se contentent pas de reproduire des modèles appris, mais développent une véritable compréhension des concepts mathématiques.” Ainsi, de grands noms des mathématiques à l’instar de Terence Tao et Timothy Gowers ont validé cette méthode.
Camernews explique : “Pourquoi FrontierMath est-il si difficile pour les modèles d’IA ? Les problèmes de FrontierMath nécessitent des connaissances spécialisées et un raisonnement créatif, ce qui est souvent difficile pour les modèles d’IA actuels, qui manquent de la compréhension contextuelle d’un expert humain.”


Et aussi, ce mois-ci...
- Notons que Pour la Science a repris deux traductions d’articles de Quanta magazine :
- Preuves informatiques : vérifier sans révéler et de façon aléatoire est désormais possible – “Les informaticiens savaient déjà comment prouver la véracité d’une affirmation sans révéler d’informations sur celle-ci, ou la vérifier en n’en examinant que de petits extraits pris au hasard. Ils ont désormais réussi à combiner ces deux approches en mettant au point une méthode de preuve « vérifiable de façon probabiliste et à divulgation nulle de connaissance ». Un tour de force en informatique théorique, qui ouvre de nouvelles perspectives pour la sécurité informatique.”
- Un problème sur les facteurs premiers d’une somme progresse après des décennies de blocage – “Comment se comportent les facteurs premiers d’une somme ? Cette question simple qui relie nombres premiers, addition et multiplication est au centre de plusieurs conjectures redoutables en théorie des nombres. Une nouvelle estimation de la croissance des facteurs premiers des nombres de la suite \(n^2+1\) a été établie, et laisse espérer des progrès dans la résolution de la célèbre conjecture abc.”
- Le magazine CNET s’interroge quant à lui sur l’utilisation de l’IA pour les mathématiques, en se focalisant sur les travaux de chercheurs de Meta
- Sciences et Avenir s’est lui penché sur les travaux de mathématiciens de l’université d’Oxford sur la dispersion “spectaculaire” des graines du concombre du diable
Enseignement
Le choc des savoirs : où en est-on des groupes de niveau ?
Alors que le Gouvernement veut poursuivre dans sa lancée en mettant en place des groupes de niveau à partir du collège, le Conseil d’État pourrait empêcher cette mesure d’être appliquée. En effet le rapporteur public du Conseil d’État vient de demander l’annulation des groupes de niveaux et a rendu publiques ses conclusions ce mercredi 20 novembre, qui ont été relayées par de nombreux médias. Pour le Conseil d’État, si cette mesure n’est pas contraire au principe du collège unique, il est nécessaire qu’elle soit prise par décret par le Premier ministre et non par arrêté par le ministère de l’Éducation nationale.
Cette annulation sera effective à partir de la rentrée 2025.
De nouvelles mesures pour les collèges et les lycées.
La ministre de l’Éducation nationale a annoncé qu’à partir de juin 2026, les élèves de première vont devoir passer une nouvelle épreuve anticipée pour le baccalauréat : l’épreuve de mathématiques. Dans un article du Monde, on peut lire qu’aucune information n’a pour l’instant été dévoilée sur le format de l’épreuve : ni son coefficient ni son programme ne sont connus. En terminale, les élèves qui ont gardé la spécialité maths passeront une deuxième épreuve l’année d’après, au même titre que toutes les autres épreuves de spécialité.
Après toutes ces réformes qui viennent modifier la manière dont sont enseignées les mathématiques, Mélanie Guenais, Sylvain Broccolichi et Cécile Allard reviennent sur la place des mathématiques en France dans un podcast de 38 minutes disponible sur Radio France.
Classement PISA : quelles causes ?
Le niveau en mathématiques des Français est tout autant une préoccupation qu’il y a deux ans, lors de la dernière enquête PISA. Jean-Marc Vittori, éditorialiste aux Échos, espère dans sa chronique du 26 novembre que ces mauvais classements en continu – il y affirme même que le niveau est en grande baisse depuis les années 90, avant la mise en place de l’étude – motivent un grand changement de l’enseignement des mathématiques en France, comme cela a été le cas en Allemagne, au Portugal ou en Pologne.
Pour lui, une possible cause de ce phénomène est un enseignement pas assez progressif : les 4/5e des profs de primaire ne sont pas formés en mathématiques, alors que ce serait le moment idéal de bien commencer la discipline, afin de pouvoir gagner en rigueur et en abstraction au fil des années.
Dans cet article du café pédagogique, Anne-Cécile Mathé, didacticienne, confirme le propos : en géométrie spécifiquement – son domaine d’expertise – on ne prend pas le temps d’apprendre aux élèves la construction en géométrie, la visualisation de celle-ci, son vocabulaire puis son abstraction, son utilisation dans des démonstrations logiques de manière assez progressive, ou assez complète.
Vittori mentionne aussi une “aridité” dans l’enseignement mathématique français : il y aurait les “forts” en maths, et les autres que le système actuel laisse derrière. Et puis, évidemment, il mentionne le manque de professeurs, entre autres car la majorité des profils matheux se tournent vers des domaines plus attractifs à bac+5, ceux du secteur privé.
Pourtant, l’enseignement mathématique est essentiel pour les révolutions numériques et énergétiques à venir. Ainsi, les besoins en ingénieur·e·s qui vont croître dans les prochaines années. Mais cela n’est pas sans rappeler que déjà aujourd’hui, nous vivons une période de manque terrible de ces profils, comme Le Monde explique dans cet article.
L’importance de la transmission des mathématiques
Pour le mathématicien David Bessis, mentionné dans cet article de Quanta Magazine, tout le monde est pourtant capable de mathématiques. Pour lui, “que vous en soyez conscient ou non, vous faites constamment des mathématiques et que vous êtes capable d’étendre vos capacités mathématiques bien au-delà de ce que vous pensez possible”. Il développe son idée dans son livre : Mathematica: A Secret World of Intuition and Curiosity. Il propose une vision des mathématiques plus basée sur l’intuition que sur la logique scolaire.
La France n’est pas le seul pays à s’inquiéter de son niveau en mathématiques, et du manque d’attractivité de celles-ci. Coumba Saar, mathématicienne sénégalaise, a mentionné, dans son interview a SciDev.Net, son intervention à la 11e édition du HLF. Elle y avait parlé de communication des mathématiques qui s’adapterait plus à l’interlocuteur, pour être plus attrayante.
À l'honneur
Lauréats des prix du Collège de France
Comme chaque année le Collège de France a décerné une série de prix à des chercheurs et des chercheuses. Deux mathématiciens et deux mathématiciennes ont été récompensés.
Tout d’abord, le cours Claude-Antoine Peccot distingue tous les ans “de jeunes mathématiciens de moins de 30 ans s’étant distingués dans l’ordre des mathématiques théoriques ou appliquées”. Deux mathématiciens sont lauréats cette année : Cyril Letrouit, du laboratoire de Mathématiques d’Orsay, et Omar Mohsen, de Paris-Saclay université.
Le premier “cherche à comprendre comment la géométrie d’un objet influe sur ses propriétés physiques”, selon le site du Collège de France. Mais il s’intéresse en parallèle à l’IA notamment pour comprendre le fonctionnement des grands réseaux de neurones artificiels. Le second “s’intéresse aux équations aux dérivées partielles et à la géométrie sous-riemannienne, qu’il étudie en utilisant des méthodes de la géométrie non commutative et les algèbres d’opérateurs”, de même selon sa présentation sur le site du Collège de France.
Une version internationale de ce prix (Cours Peccot International) récompense depuis 2023 “de jeunes mathématiciennes européennes, invitées à donner une série de conférences au Collège de France”. Et c’est Lisa Sauermann, professeure à l’université de Bonn, qui a reçu le prix cette année. Elle s’illustre en combinatoire, en algèbre et en théorie des probabilités. Elle interviendra du 4 février au 10 mars 2025 au Collège de France pour une conférence intitulée “Three-term arithmetic progressions, the slice rank polynomial method and the Erdös-Ginzburg-Ziv Problem”.

Lisa Sauermann
Pegah Pournajafi, ATER au Collège de France, est la quatrième personne spécialiste des mathématiques distinguées par le Collège de France. Elle a reçu le prix de la Fondation Hugot du Collège de France qui favorise “la rencontre des diverses disciplines qui œuvrent à la connaissance, à la formation et à l’épanouissement de l’homme”. Il récompense des ATER au Collège de France. Les diverses disciplines que Pegah Pournajafi fait se rencontrer sont la combinatoire, la géométrie et les algèbres d’opérateurs. Le Collège de France note : “Au fil de ses études, elle a développé un goût marqué pour la recherche interdisciplinaire en mathématiques, combinant la combinatoire avec des outils et concepts issus de domaines variés.”
Prix Irène Joliot-Curie

Sylvie Méléard
Le prix Irène Joliot-Curie récompense une femme scientifique qui a “apporté une contribution remarquable dans le domaine de la recherche”. Cette année c’est Sylvie Méléard, professeur à l’X, qui a reçu ce prix. Elle s’illustre à l’interface entre mathématiques et biologie.
Comme il est expliqué sur le site de l’École Polytechnique : “Son expertise en probabilités apporte un point de vue nouveau et original aux biologistes pour étudier les dynamiques de populations, qu’il s’agisse d’émergence d’espèces, de croissance de populations bactériennes ou encore de développement de cellules. Grâce à un formalisme qui intègre les comportements aléatoires (naissance, mutation, compétition, etc.) elle conçoit avec ses collègues des modèles permettant de donner un résumé mathématique de ces mécanismes.”
Dixième anniversaire du décès d’Alexandre Grothendieck

Alexandre Grothendieck
Le 13 novembre 2014 disparaissait Alexandre Grothendieck. Plusieurs médias ont donc mis à l’honneur ce “génie engagé”.
Le Journal du CNRS a, par exemple, rencontré Leila Schneps, directrice de recherche CNRS à l’Institut de mathématiques de Jussieu – Paris rive gauche. Dans une longue interview, la mathématicienne explique les travaux de Grothendieck et raconte son héritage sur les mathématiques modernes.
Touchant témoignage où elle partage également ce que sa rencontre avec Grothendieck a eu comme conséquence sur sa carrière : “En mathématiques, on a tous peur de ne pas réussir, de rater, de se tromper, d’investir un temps fou pour rien… Grothendieck m’a fait prendre conscience de cette peur en moi. Et il m’a appris à la combattre en laissant surgir en moi la simple joie de la découverte.”
Leila Schneps fait partie de celles et ceux qui rassemblent des archives du mathématicien sur le site Grothendieck-circle.org. “En 1991, Esquisse d’un programme m’est tombé entre les mains, puis Récoltes et Semailles. J’avais vraiment envie de lire d’autres textes de cet auteur. Et j’ai appris que plusieurs personnes avaient en leur possession des lettres, ou des notes, ou avaient simplement rencontré et partagé avec Alexandre Grothendieck. Un jour, en 2003, on s’est retrouvé dans un café à Paris et on a décidé de créer le Grothendieck circle pour rassembler tous les documents à un endroit.”
De son côté, l’Institut des hautes études scientifiques (IHES) – où Grothendieck a travaillé – a republié la vidéo d’un cours donné en 1996 par le mathématicien Pierre Deligne. Celle-ci porte sur les six opérations de Grothendieck. Notons d’ailleurs que l’IHES organise une soirée le 6 février 2025 sous l’intitulé “Alexandre Grothendieck, de la légende mathématique à l’inspiration littéraire” (événement gratuit mais l’inscription est obligatoire).
Le Midi Libre se souvient également de celui qui fut l’un des habitants de cette région dans un article publié ce mois-ci. Avec des témoignages de ses proches, il y parle de sa personnalité et son engagement politique.


Et aussi, ce mois-ci...
- L’université de Cambridge annonce la nomination de la première professeure de “compréhension publique des mathématiques”. Il s’agit de Hannah Fry, une mathématicienne, autrice et animatrice d’émission de télévision et de podcast. “L’objectif ultime est de contribuer à créer une population plus sensible et à l’aise avec les concepts mathématiques. “
- L’Académie des Sciences a mis en ligne le discours de Cédric Villani prononcé en mai 2024 “lors d’une séance consacrée à l’installation du prix Maurice-Audin”
- L’université de Genève fête quant à elle ses “300 ans de mathématiques” et a organisé un évènement à la fin du mois à cette occasion.
Diffusion
Le Mois des Mathématiques Appliquées et Industrielles (M2AI).
Organisé par la Société de Mathématiques Appliquées et Industrielles (SMAI), le mois des mathématiques appliquées et industrielles (M2AI) est une initiative annuelle qui vise à promouvoir les mathématiques appliquées auprès d’un large public. Composé de quatre conférences, étalées sur plusieurs semaines, cet événement explore des thématiques variées illustrant le rôle des mathématiques dans des secteurs clés comme l’industrie, l’ingénierie et la recherche scientifique.
Sensibiliser aux stéréotypes de genre.
L’exposition “Just Do Maths !”, organisée par l’Université Paris-Saclay, met à l’honneur des mathématiciennes en brisant les stéréotypes liés au genre dans cette discipline. Prévue pour circuler en 2024 et 2025 à travers divers établissements de Paris-Saclay, cette exposition présente des portraits inspirants de femmes scientifiques.
L’objectif de cette initiative est double : sensibiliser le public aux inégalités de genre dans les domaines scientifiques et valoriser les recherches et les carrières de mathématiciennes de l’Université Paris-Saclay.
Les Échappées inattendues du CNRS : une immersion scientifique créative à Lyon
Ce 15, 16 et 17 Novembre, le Collège Truffaut a accueilli les Échappées inattendues du CNRS, un événement combinant science et créativité. Au cours de leur visite, les visiteur⋅ses ont l’occasion de percer les mystères des odeurs, se promener le long d’un pétale ou encore sonder les nuages à l’échelle microscopique. En associant art et science à travers ces thèmes variés, cette initiative permet d’engager un dialogue accessible et ludique sur des enjeux majeurs : santé, réchauffement climatique, et innovation technologique. Les conférences sont disponibles en replay sur YouTube.


Et aussi, ce mois-ci...
- La plateforme Carmin.tv propose plus de 7000 vidéos issues de conférences pour promouvoir les mathématiques. (Source)
- Un podcast explore la portée universelle des mathématiques avec deux chercheuses engagées dans leur transmission. (RFI)
- Étienne Ghys explore les liens entre mathématiques et langage, soulignant leur universalité et leur interconnexion. (Le monde)
- Cédric Villani célèbre la beauté culturelle et scientifique des mathématiques dans sa chronique dédiée. (Humanité)
- Le podcast Maths en Tête célèbre ses trois ans avec deux nouveaux épisodes pour continuer à vulgariser les mathématiques. (lien)
- Un épisode hispanophone revient sur les apports révolutionnaires d’Évariste Galois dans la théorie des groupes. (Youtube)
- Une vidéo pédagogique explique les origines des nombres décimaux et la contribution de Simon Stévin. (Mathix)
- L’exposition Mathématiques du quotidien à la Maison Poincaré illustre l’impact historique et pratique des mathématiques dans notre quotidien. (Réservation)
Parutions
En kiosque, on retrouve…
Comme chaque mois, on a plaisir à retrouver Jean-Paul Delahaye dans la revue Pour la Science. L’article de ce mois-ci porte sur les “ordinateurs origamis” – oui ces petits pliages de papier ! “On montre facilement qu’en pliant du papier on peut aussi, partant d’une feuille carrée de côté 1, déterminer par pliage des points distants l’un de l’autre de √n pour tout entier n – on dit que ces nombres sont « constructibles par origami ». Cette sorte de « calcul par origami » est aujourd’hui bien comprise et, avec une certaine surprise, on a découvert que cela donnait en fait accès à davantage de nombres que les constructions à la règle et au compas : ∛2, par exemple, est constructible par origami”, explique-t-il.

Mais en 2023, Thomas Hull, du Franklin and Marshall College, et Inna Zakharevich, de l’université Cornell, vont plus loin en démontrant que l’origami est Turing-complet ou computationnellement universel : “Pour toute fonction calculable f de l’ensemble des entiers vers lui-même telles qu’elles ont été définies par Alan Turing en 1936, il existe un pliage qui réalise le calcul de f.”
La démonstration de ce résultat est née dans l’esprit d’Inna Zakharevich quand elle “a découvert qu’une démonstration du même type existait pour le jeu de la vie, imaginé par John Conway”.
Pour Thomas Hull, cela pourrait avoir des conséquences en mathématiques : « Plus nous ferons de choses comme celles-ci, plus je pense que nous aurons de chances d’établir des croisements profonds entre l’origami et des branches bien établies des mathématiques. »
Leur article est un préprint à retrouver ici.
Restons du côté de Pour la Science qui s’est lancé la mission de capturer l’infini dans les 124 pages de son Hors-Série sorti au début de ce mois.

Un entretien est donné à Jean-Paul Delahaye (encore lui !) où il remonte aux origines de l’infini. “Dès que fut disponible une forme de numération de position, comme la nôtre, où la signification d’un chiffre dépend de sa position dans le nombre, et à l’inverse du système romain par exemple, il me semble que de façon implicite, on a eu accès à l’infini.” De même, avec la notion de droite vient directement celle de l’infini. Mais cela n’a pas empêché que cette idée soit difficile à capturer : “Qu’il puisse y avoir autant d’entiers (positifs) pairs que d’entiers apparaissait paradoxal. La notion d’infini en acte semblait donc contradictoire, et on la laissait prudemment à Dieu, le seul à pouvoir penser l’infini !” Les travaux de Cantor du XIXe siècle vont changer la donne.
Au programme du reste du numéro : l’existence ou non d’un infini intermédiaire entre celui des nombres entiers et celui des nombres réels, de la géométrie, des “querelles des infinitésimaux”, la perspective. Et aussi de l’infini en physique et en cosmologie.
Ouvrons un autre magazine, celui de Sciences et Avenir pour y lire la contribution d’Antoine Houlou-Garcia. Dans la continuité de son livre Il était une fois le zéro, il propose de démêler le vrai du faux de l’interdiction du zéro au Moyen-Âge. “On imagine volontiers que l’Église a interdit (ou au moins lutté contre) les chiffres arabes, symboles du monde musulman honni, et en particulier le zéro, symbole diabolique d’un vide pouvant menacer la création divine. De fait, s’ils étaient connus dès 773 à Bagdad, il fallut des siècles pour que l’Occident accepte leur usage. Derrière cette idée implicite d’un choc des civilisations et d’un Moyen Âge obscurantiste se cache néanmoins une vérité plus subtile.”

En librairie
À l’occasion de la publication de son dernier livre – au sujet duquel nous écrivions le mois dernier – L’équation de la chauve-souris – de la poussée d’Archimède à la physique quantique, Mickaël Launay a été l’invité du podcast La Science, CQFD.
L’auteur (et youtubeur !) répond à des questions telles que « Peut-on vraiment voir toutes les choses du quotidien sous le prisme des maths ? », “Quelle est l’importance du changement de point de vue en mathématiques ?” ou encore «C’était quoi votre dernier émoi mathématique ? ». À cette occasion sont évoqués des sujets aussi divers que l’esthétisme, l’abstraction, la géométrie projective, l’essor du nombre en Mésopotamie, les pavages…
Autre bijou de vulgarisation, ce mois-ci est paru Réalise des jeux scientifiques inspirés des grands mathématiciens, édition française de Math for kids de Rebecca Rapoport et Allanna Chung, traduite par Claire Cadet. Son mot d’ordre : s’initier aux maths en s’amusant. Le principe : après le portrait d’un·e mathématicien·ne s’ensuit une activité pour découvrir de façon ludique des mathématiques qui touchent à son sujet de recherche. À découvrir à partir de 7 ans !
Et si, au lieu de faire des maths, on se les laissait conter ? C’est ce qu’offre la lecture du nouvellement paru Les maths comme je les aime et comme je les raconte ! de Philippe Colliard. Le professeur agrégé de mathématiques et membre du comité éditorial d’Images des maths nous raconte les mathématiques comme il les aime, sous forme de dialogues, posant des questions simples telles que : qu’est-ce qu’un point ? dont la réponse est bien difficile à formuler… et pourtant claire sous la plume de l’auteur.
Pour finir
Nous vous recommandons l’article d’une interview donnée au Monde par la mathématicienne Laure Saint-Raymond. Le sujet n’est pas sa carrière, mais plutôt sa parentalité en tant que professeure, que mathématicienne et en tant que chercheuse.


16h04
Je suis amoureux de Conway donc je souffre de l’existence de ce contre-exemple qui est un nombre cyclique en quelque sorte.
16h05
Ne pourrait-on pas sauver la conjecture de Conway en disant que cette procédure permet de tomber ou sur un nombre premier ou sur le nombre lui-même?