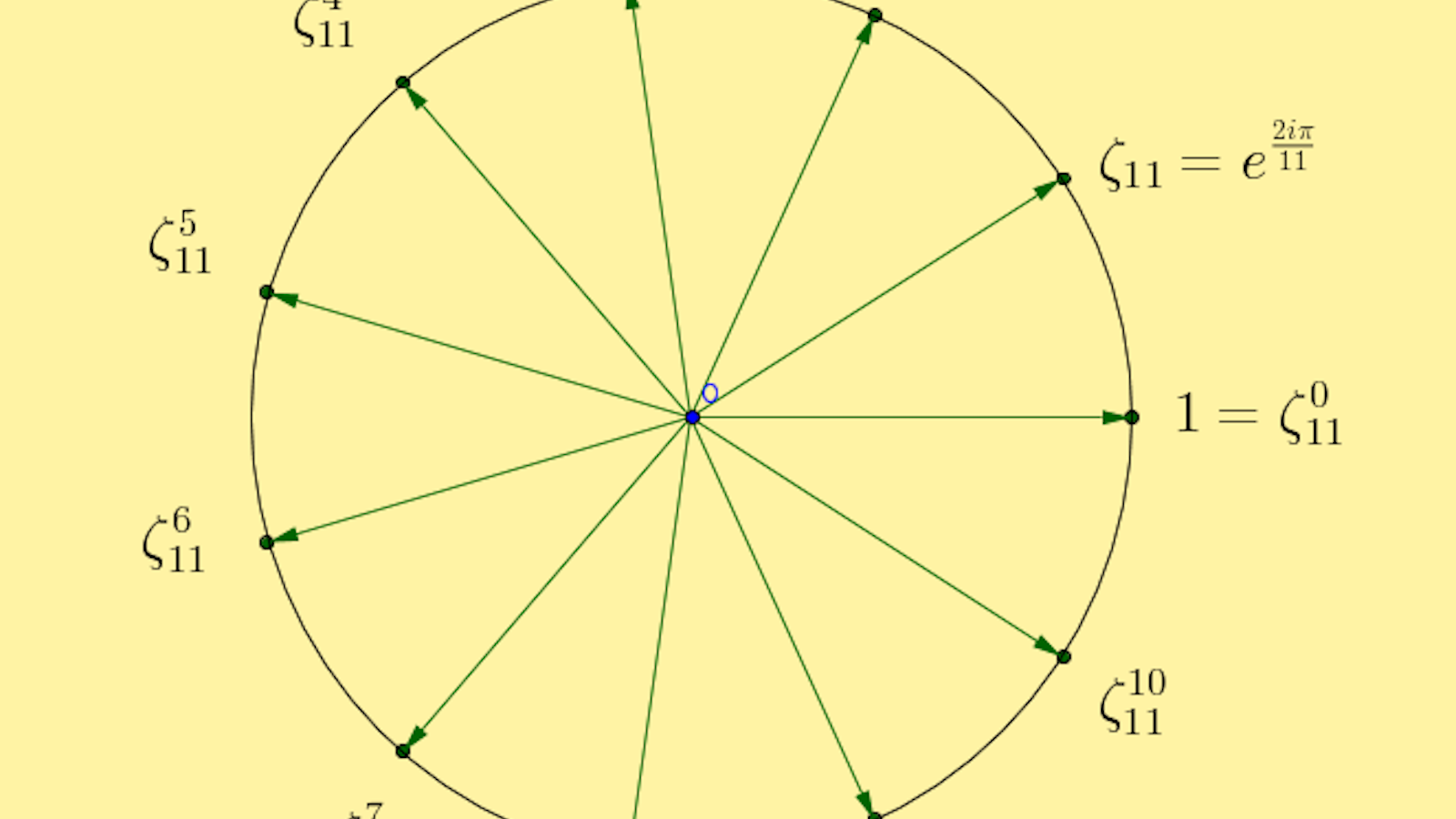
Nous présentons ici un résultat de Pierre Deligne, un peu ancien, mais, nous semble-t-il, compréhensible à qui sait ce qu’est un nombre complexe et une racine complexe de l’unité. Au programme en 2013 : un problème de comptage d’analogues d’équations différentielles, sur certains objets géométriques et arithmétiques, et toute une série d’exposés sur ce problème. Il y a encore beaucoup de problèmes à résoudre à propos de cette question récente, ce qui fera dire à Deligne qu’il allait aussi expliquer ce « qu’il ne connaissait pas » de ce problème de comptage.
ÉCRIT PAR
Christine Huyghe
Directeur de Recherche CNRS - l'Université de Franche-Comté (Besançon)
