Nous entendions ce matin à la radio qu’il devait y avoir une erreur dans les modèles mathématiques (en fait dans LE modèle, britannique, décrié par les journalistes), puisque les vols d’essais menés par plusieurs compagnies aériennes semblent avoir laissé les moteurs dans un état intact.
Nous allons essayer de décrypter cette affirmation.
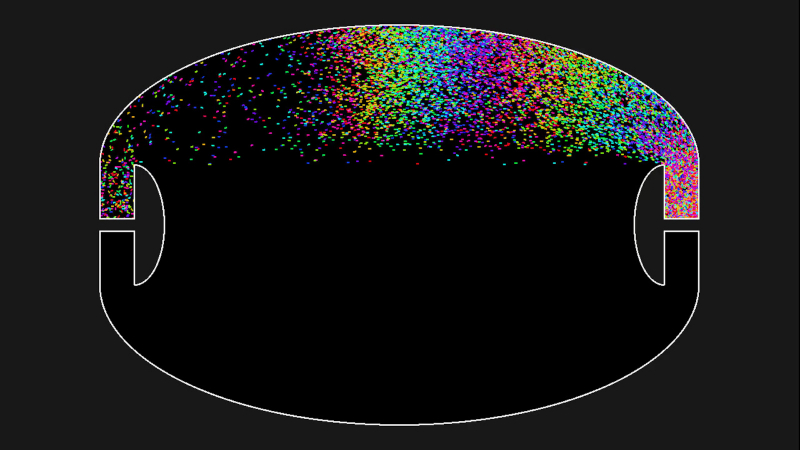
Depuis quelques jours, nous pouvons consulter sur la toile des images satellites de la progression des cendres dans l’atmosphère (Source : Met Office).

.

.
Notons au passage que les météorologistes britanniques sont reconnus comme faisant partie des meilleurs au monde (mentionnons, par exemple, que le centre européen de météorologie (ECMWF) se situe à Reading, près de Londres). Nous pouvons donc avoir une assez bonne confiance dans le travail qu’ils effectuent.
Par ailleurs, et il convient ici de bien faire la différence, nous pouvons aussi observer des cartes prévisionnelles (calculées avec un modèle) de la progression des particules de cendre éjectées par le volcan.

Prévision du 19 avril
Dans ce qui suit, nous allons faire une description assez simple des concepts contenus dans ces modèles, (bien sûr, un nombre certain d’approximations sera fait implicitement et les spécialistes pourront s’élever contre elles, mais l’on souhaite rester ici le moins technique possible) en gageant toutefois qu’elle reflète assez bien ce qui est effectué en pratique.
Le modèle mathématique utilisé est de la forme suivante : il décrit, à l’aide d’une équation que nous n’écrirons pas, l’évolution de la concentration de particules dans l’espace et dans le temps. Autrement dit, il peut nous dire à quel endroit et en quelle quantité se trouve les particules éjectées par le volcan (noté, la source, dans ce qui suit), à divers instants (disons \(T_0\), \(T_1\), \(T_2\), etc) . Avec les mains, nous pouvons dire que :
$$
\begin{array}{c}
variation \; en\\
temps \; de \; la\\
concentration
\end{array} = \begin{array}{c}
déplacement\\
induit \; par \\
le \; vent
\end{array} + \begin{array}{c}
diffusion \; des\\
particules
\end{array} + \begin{array}{c}
source \; du \\
volcan
\end{array}
$$
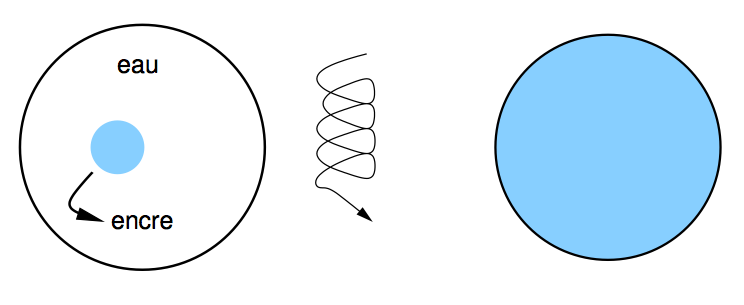
Précisons quelques points. Nous rappellons que la concentration dépend de l’espace et du temps (penser au nuage des particules qui se déplace sur les images précédentes). L’un des moteurs qui fait se déplacer la concentration est bien sûr le vent qui souffle dans l’atmosphère. La source n’est rien d’autre que le “robinet” qui alimente l’atmosphère en particules. Le terme de diffusion est celui qui demande peut être une explication : il peut se comprendre avec l’exemple d’une goutte d’encre dans un verre d’eau :
.
si on dépose une goutte d’encre en un point, elle va se propager (si l’on agite le liquide, la progression sera plus rapide) dans tout l’espace qui la contient. Ce phénomène s’applique aussi (en 3 dimensions et non en 2 comme sur le dessin) aux cendres que le volcan “dépose” dans l’atmosphère, à la différence que le flux est ici continu dans le temps (il n’est pas déposé qu’une seule “goutte” de cendre).
Comme pour tout modèle, il contient des paramètres. Brièvement, il existe un paramètre qui décrit la capacité plus ou moins rapide des particules à se répandre dans le milieu ambiant (on parle d’un coefficient de diffusion), de plus, il faut connaitre la vitesse du vent dans l’atmosphère (ici, on peut se servir des mesures réelles, ou utiliser des vitesses calculées par un autre modèle (cf. l’article d’Isabelle Gallagher)) et enfin, il faut donner une condition initiale au modèle, c’est-à-dire l’état de la concentration à l’instant \(T_0\) pour que la simulation possède une quantité qu’elle fera ensuite évoluer grâce à un calcul sur ordinateur. Avec une même équation, il est clair que si les paramètres sont différents, les solutions prévues par le calcul seront donc différentes.
On peut ainsi dire que le modèle mathématique, en terme d’équations (c’est-à-dire en terme de la compréhension des phénomènes prépondérants qui pilotent l’évolution de la concentration des particules) est raisonnablement juste. En revanche, il est souvent difficile d’en déterminer précisément les paramètres (pour de nombreuses bonnes raisons que nous ne décrirons pas dans ce billet 2mais qui, notons-le, sont à l’origine de recherches mathématiques actuelles et variées) et c’est ce qui explique que les simulations/prévisions peuvent êtres différentes.
Quoi qu’il en soit, il est aussi raisonnable de penser qu’au niveau européen les météorologistes et leurs collègues travaillent en commun et que les prévisions de la position des cendres du volcan sont relativement homogènes d’un centre à l’autre (Met Office, Météo France, etc). Un autre élément qui est, de surcroît, à prendre en compte est le “critère de sûreté” adopté pour les autorisations de vol. Le calcul donne la position mais aussi, la quantité de particules. Donc si les critères se basent sur des quantités maximales de cendres, tolérées par les moteurs, différentes, il peut aussi en découler des autorisations de vols distinctes suivant le lieu géographique.
Post-scriptum
Nous pouvons quand même, juste pour le plaisir des yeux, écrire l’équation aux dérivées partielles correspondant à la description ci-dessus :
$$
\partial_t \, c(x,t) = v(x,t) \nabla c(x,t) + \nabla . (d \nabla c(x,t)) + f(x,t).
$$
Le coefficient de diffusion est \(d\), les mouvements atmosphériques apparaissent dans \(v\) et la source constitue le \(f\). Les dépendances en espace et en temps se lisent dans les arguments \((x,t)\) (que l’on aurait pu d’ailleurs aussi attribuer à \(d\) si la nature du conglomérat de cendres change au cours du temps).