
La rubrique s’adresse à tous ceux, petits et grands, qui souhaitent s’amuser tout en faisant des mathématiques, autour de thèmes parfois oubliés des programmes scolaires. Les connaissances utiles sont celles d’un élève de collège ou de lycée. Le cœur de cette rubrique est formé d’une petite série de thèmes choisis, dont chacun se parcourt travers un déroulé de problèmes.
Dans chaque article, certains problèmes sont accompagnés de solutions. Les solutions des autres problèmes seront mises en ligne deux semaines après la publication de l’article.
Les meilleures solutions seront publiées dans la rubrique.
Le professeur Euler retrouve ses étudiants de la planète Mars (voir Graphes 1). Il peut cette fois être présent parmi eux pour donner son cours car, entre temps, l’Agence des navettes interplanétaires du système solaire, par souci d’efficacité, mais aussi par souci d’économie, a mis au point un nouveau réseau respectant le principe suivant : deux planètes quelconques du système solaire doivent être reliées par un et un seul itinéraire (on suppose qu’un itinéraire n’emprunte pas deux fois la même ligne de navettes). Le professeur fait part de cette bonne nouvelle à ses étudiants et leur déclare, qu’en plus de lui permettre d’être là avec eux, cela lui donne une belle occasion de leur présenter un type particulier de graphes. Il précise aussi que, dans toute cette leçon, les graphes étudiés seront finis, sans boucle, et tels que deux quelconques de leurs sommets seront joints par une arête au maximum.
Problème 1. Efficacité et économie
Le réseau des liaisons par navettes spatiales entre les treize planètes du système solaire a la propriété décrite dans l’introduction de cet article : entre deux quelconques de ses planètes, il existe un et un seul itinéraire possible, via éventuellement une ou plusieurs autres planètes. Montrer que, dans ce réseau, il est impossible de trouver un itinéraire partant d’une planète et y revenant sans emprunter deux fois une même liaison.


Solution (à lire avant de poursuivre la lecture de l’article)
Supposons qu’il existe un itinéraire partant d’une planète du système solaire (appelons-la X) et y revenant sans avoir emprunté deux fois la même liaison du réseau. Le graphe associé au réseau n’ayant aucune boucle, il existe au moins une planète du système solaire (appelons-la Y) par laquelle passe cet itinéraire. Cela implique qu’il existe deux itinéraires différents pour aller de la planète X à la planète Y : un premier en suivant la partie du cycle qui mène de X à Y, un deuxième en suivant à rebours la partie du cycle qui va de Y à X. Il y a là une contradiction, car entre deux quelconques des planètes, il n’y a qu’un seul itinéraire possible. Il est donc impossible de trouver un itinéraire partant d’une planète et y revenant sans emprunter deux fois une même liaison du réseau.
Rappelons deux notions abordées par le professeur Euler dans sa première leçon : la notion de connexité et la notion de cycle.
- Un graphe est dit connexe si, pour chaque paire de ses sommets, il existe un chemin qui les relie.
- Un cycle dans un graphe est un chemin élémentaire (un chemin qui n’emprunte pas deux fois la même arête) et tel que son début coïncide avec sa fin.
La résolution de ce premier problème permet donc d’affirmer que le graphe associé au nouveau réseau des navettes interplanétaires ne possède aucun cycle. Il est clair aussi que ce graphe est connexe, puisqu’entre deux quelconques des planètes, il existe un itinéraire. Un tel graphe, connexe et sans cycle, est appelé un arbre.
Retenons alors la définition suivante.
Un arbre est un graphe connexe sans cycle.
Le professeur Euler ajoute que la solution du problème 1 se généralise et permet d’énoncer le résultat suivant.
Un graphe dans lequel deux sommets quelconques sont reliés par un et un seul chemin élémentaire est connexe et n’a pas de cycle ; c’est donc un arbre.
Problème 2. Arbre ou pas arbre
Parmi les graphes suivants, lesquels sont des arbres ?
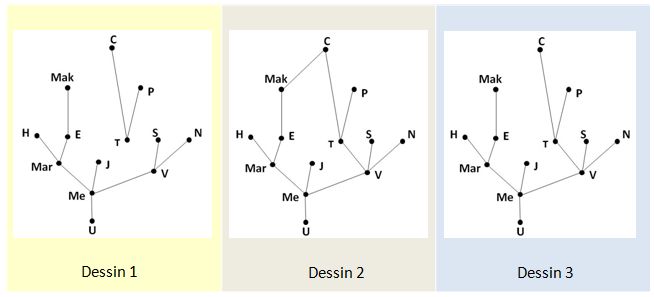


Solution
Le graphe du dessin 1 n’est pas un arbre car ce graphe n’est pas connexe. Il a deux composantes connexes.
Le graphe du dessin 2 n’est pas un arbre car, dans ce graphe, il y a le cycle Me-Mar-E-Mak-C-T-V-Me.
Le graphe du dessin 3 est un arbre car c’est un graphe connexe sans cycle.
Le professeur Euler fait remarquer à ses étudiants qu’on peut donner une deuxième définition d’un arbre.
Un arbre est un graphe dans lequel deux sommets quelconques sont reliés par un et un seul chemin élémentaire.
Il leur laisse le soin de démontrer l’équivalence de ces deux définitions d’un arbre.
Problème 3. Départ d’une seule navette
Supposons que le graphe des correspondances entre les 13 planètes du système solaire soit un arbre. Montrer que, parmi ces treize planètes, il en existe au moins une d’où il ne part qu’une seule navette.


Solution (à lire avant de poursuivre la lecture de l’article)
Considérons l’arbre représentant les correspondances entre les 13 planètes. De chaque sommet de l’arbre part au moins une arête, car l’arbre est, par définition, connexe. Notre objectif est de trouver un sommet d’où part exactement une arête. Pour cela, commençons par un sommet quelconque et construisons un chemin qui part de ce sommet en suivant des arêtes au hasard sans jamais rebrousser chemin. Notons qu’il est impossible de revenir à un sommet déjà visité, car nous aurions alors découvert un cycle dans l’arbre, or on sait qu’il n’y en a pas. Comme le nombre d’arêtes est fini, cela signifie qu’à un moment il sera impossible de continuer notre chemin. Du dernier sommet du chemin partira alors exactement une arête, car sinon on aurait pu continuer le chemin en empruntant une arête différente de celle par laquelle on est arrivé à ce sommet.
Ce problème se généralise très aisément et permet d’énoncer un résultat relatif aux arbres.
Dans un arbre ayant au moins deux sommets, il en existe toujours au moins un d’où ne part qu’une seule arête. Un tel sommet est dit suspendu.
Problème 4. Puissance 5
On considère un graphe dont chaque sommet est de degré 5. Montrer que ce graphe possède au moins un cycle.


Solution
Ce graphe n’est pas un arbre, car il a au moins deux sommets et aucun n’est suspendu. Donc, s’il est connexe, il a nécessairement un cycle. S’il n’est pas connexe, considérons une de ses composantes connexes. Cette composante connexe a au moins deux sommets et aucun d’eux n’est suspendu ; elle n’est donc pas non plus un arbre. Comme elle est connexe, elle possède au moins un cycle.
NB : cette démonstration aurait pu être faite sans disjonction de cas, en considérant qu’un graphe connexe possède lui aussi une composante connexe. Cette composante connexe est unique : c’est le graphe tout entier.
Afin d’introduire une nouvelle propriété des arbres, le professeur Euler propose à ses étudiants le problème suivant.
Problème 5. Combien de lignes directes ?
Sachant que le graphe des correspondances entre les 13 planètes du système solaire est un arbre, combien le réseau des navettes interplanétaires a-t-il de lignes directes (lignes reliant deux planètes sans escale) ?


Solution (à lire avant de poursuivre la lecture de l’article)
Considérons l’arbre représentant les lignes entre les 13 planètes. Cet arbre possède au moins un sommet suspendu. Enlevons un sommet suspendu ainsi que l’arête qui part de ce sommet. Le nouveau graphe est encore un arbre (puisqu’il est toujours connexe et sans cycle). Cet arbre possède à son tour au moins un sommet suspendu. Enlevons encore une fois un sommet suspendu avec l’arête qui part de ce sommet et répétons cette opération jusqu’à obtenir un graphe avec un seul sommet. Ce graphe est donc sans arête. Puisqu’à chaque opération nous avons enlevé un sommet et une arête, le graphe initial avait exactement un sommet de plus que d’arêtes. Il existe donc exactement 12 lignes reliant directement deux planètes.
Il est clair que ce problème, par sa généralisation, autorise l’énoncé du théorème suivant.
Dans un arbre, le nombre A d’arêtes est égal au nombre S de sommets diminué de 1 :
A = S – 1.
Les étudiants du professeur Euler se demandent si ce théorème possède une certaine forme de réciprocité. Le professeur Euler confirme qu’effectivement cette réciproque existe dans l’ensemble des graphes connexes. Il propose de s’en convaincre en résolvant le problème suivant.
Problème 6. Arbre ou pas arbre ?
Montrer qu’un graphe connexe dont le nombre d’arêtes est égal au nombre de sommets diminué de 1 est un arbre.


Solution (à lire avant de poursuivre la lecture de l’article)
Supposons que ce graphe ne soit pas un arbre. Comme il est connexe, il possède nécessairement au moins un cycle. Enlevons une arête d’un tel cycle. Le nouveau graphe obtenu est encore connexe. Si ce nouveau graphe n’est pas un arbre, c’est qu’il possède encore un cycle duquel on peut enlever une arête en préservant la connexité. On continue ainsi la procédure jusqu’à épuisement des cycles. Le graphe alors obtenu est connexe sans cycle : c’est donc un arbre. Pour cet arbre, nous avons la relation A = S – 1, où A est le nombre de ses arêtes et S le nombre de ses sommets. Dans toutes ces opérations, aucun sommet du graphe initial n’a disparu. Le nombre S est donc aussi le nombre de sommets du graphe initial. Comme dans le graphe initial, le nombre d’arêtes est égal au nombre de sommets diminué de 1, le nombre A est aussi le nombre d’arêtes du graphe initial. Cela signifie qu’aucune arête du graphe initial n’a été effacée. Contradiction. Le graphe initial est donc un arbre.
Le professeur Euler propose maintenant à ses étudiants de terminer sa leçon en évoquant un problème dont la solution consiste à choisir un arbre « maximal » contenu dans un graphe connexe donné.
Problème 7. Fermetures pour travaux
Dans un pays, il y a 20 villes qui sont reliées deux à deux par une ligne de chemin de fer. Il n’y a pas de correspondances en dehors des villes (lorsque deux chemins de fer se rencontrent en dehors des villes, l’un d’eux passe sous l’autre par un tunnel). Quel nombre maximal de chemins de fer peut-on fermer simultanément si on veut conserver la possibilité de relier deux villes quelconques entre elles (éventuellement en passant par d’autre(s) ville(s)) ?


Solution (à lire avant de poursuivre la lecture de l’article)
Considérons le graphe dont les sommets sont les 20 villes du pays et dont les arêtes sont les lignes de chemin de fer les reliant deux à deux.`
Remarquons que dans ce graphe il y a \(\displaystyle\frac{20 \times 19}{2}\) arêtes, soit 190, car chacun des 20 sommets est de degré 19.
Remarquons aussi que le problème posé est équivalent à celui-ci :
Combien peut-on supprimer d’arêtes au maximum dans ce graphe de manière à ce que le graphe alors obtenu soit encore connexe ?
Le graphe initial n’est pas un arbre car il est connexe mais il n’a aucun sommet suspendu. Ce graphe possède donc au moins un cycle. Enlevons une arête à un premier cycle de ce graphe ; le graphe alors obtenu est toujours connexe. Poursuivons ainsi notre travail de « démolition » en enlevant une par une des arêtes au graphe, en préservant à chaque étape sa connexité. Quand on ne pourra plus enlever d’arête sans perdre la connexité, on aura un arbre. Cet arbre a 20 sommets ; il a donc 19 arêtes. Ceci prouve qu’on peut enlever 171 arêtes (190 – 19) sans perdre la connexité.
Peut-on en enlever davantage ?
Supposons qu’il soit possible d’enlever plus de 171 arêtes à ce graphe, en préservant la connexité. Lorsque les 171 premières arêtes auront été enlevées, le graphe obtenu sera connexe et possédera 20 sommets et 19 arêtes. Ce graphe est alors nécessairement un arbre (puisqu’il s’agit d’un graphe connexe vérifiant la relation A = S -1). En enlevant n’importe quelle arête de cet arbre, on obtient un graphe non connexe.
On peut donc fermer au maximum 171 lignes de chemin de fer dans ce pays, si on veut conserver la possibilité de relier deux villes quelconques entre elles.
Ainsi s’achève la deuxième leçon du professeur Euler. Sa troisième leçon portera sur les graphes planaires et sur la formule d’Euler. Avant de se séparer de ses étudiants, le professeur Euler soumet à leur sagacité les deux problèmes suivants.
Problème 8. Araignée du matin, chagrin ...
Dans cette toile d’araignée, quel nombre maximal de fils peut-on couper pour que la toile ne se divise pas en plusieurs morceaux ?
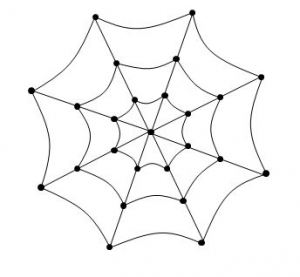


Solution
Considérons cette toile d’araignée comme un graphe dont les sommets sont les nœuds de la toile et les arêtes sont les fils. Le nombre de ses sommets est 25 et le nombre de ses arêtes est 48 (pour dénombrer les arêtes on peut, par exemple, repérer que le graphe a 8 sommets de degré 3, 16 sommets de degré 4 et 1 sommet de degré 8).
Remarquons que le problème posé est équivalent à celui-ci :
Combien peut-on supprimer d’arêtes au maximum dans ce graphe de manière à ce que le graphe alors obtenu soit encore connexe ?
Le graphe initial est connexe mais n’est pas un arbre car il possède plusieurs cycles. Enlevons une arête à un premier cycle de ce graphe ; le graphe alors obtenu est toujours connexe. Poursuivons ainsi notre travail en enlevant une par une des arêtes au graphe, en préservant à chaque étape sa connexité. Quand on ne pourra plus enlever d’arête sans perdre la connexité, on aura un arbre. Cet arbre a 25 sommets ; il a donc 24 arêtes. Ceci prouve qu’on peut enlever 24 arêtes de ce graphe (48 – 24) sans perdre sa connexité.
Peut-on en enlever davantage ?
Supposons qu’il soit possible d’enlever plus de 24 arêtes à ce graphe, en préservant la connexité. Lorsque les 24 premières arêtes auront été enlevées, le graphe obtenu sera connexe et possédera 25 sommets et 24 arêtes. Ce graphe est alors nécessairement un arbre (puisqu’il s’agit d’un graphe connexe vérifiant la relation A = S -1). En enlevant n’importe quelle arête de cet arbre, on obtient un graphe non connexe.
On peut donc couper au maximum 24 fils pour que la toile ne se divise pas en plusieurs morceaux.
Problème 9. Fermeture d’un aéroport
Un réseau de lignes aériennes est constitué de telle manière qu’il est possible de joindre deux quelconques de ses aéroports, éventuellement en faisant des escales dans d’autres aéroports du réseau. Montrer qu’on peut fermer un aéroport de ce réseau (et les lignes aériennes qui y mènent) sans perdre la possibilité de joindre deux autres quelconques aéroports du réseau.


Solution
Considérons le graphe dont les sommets sont les aéroports du réseau et dont les arêtes sont les lignes aériennes de ce même réseau. Ce graphe est connexe car il est possible de joindre par avion deux quelconques des aéroports du réseau. À l’image de ce qui a été fait dans le problème 8, nous pouvons supprimer tour à tour des arêtes dans ce graphe, tout en préservant à chaque fois sa connexité. Quand on ne pourra plus le faire, on aura un arbre. Cet arbre a un sommet suspendu : appelons-le X. Si du graphe initial, on enlève ce sommet X ainsi que toutes les arêtes qui partent de X, le graphe restant sera connexe.
Cela signifie qu’on peut fermer l’aéroport X et toutes les lignes aériennes qui en partent ou qui y arrivent sans perdre la possibilité de joindre deux autres quelconques aéroports du réseau.
Post-scriptum
Pour la rédaction de cet article, nous nous sommes inspirés de l’ouvrage « Cercles mathématiques de Leningrad » de Dimitri Fomine, Sergueï Guenkine et Ilia Itenberg, KIROV, ASA, 1994.
Article édité par Equipe de la rubrique « En sortant de l’école »




8h59
Le problème 9 me laisse perplexe. Si on relie Toulouse à Saint-Louis du Sénégal, puis Saint-Louis à Natal au Brésil, on obtient bien un graphe connexe. Mais comment Mermoz aurait-il fait avec la fermeture de Saint-Louis, si l’on s’interdit d’inventer d’autres escales ?
Pour obtenir la propriété voulue, j’aurais plutôt mis comme hypothèse que deux quelconques des aéroports sont toujours parcourus par au moins un cycle.
11h04
Bonjour,
Si on choisit de fermer Toulouse ou Natal, les deux autres aéroports peuvent toujours être reliés, donc la propriété est vérifiée sur ce graphe.
12h19
C’est l’éternel problème de l’article « un », tantôt universel, tantôt existentiel. Dans le problème 6, par exemple, il ne suffit pas de trouver un graphe connexe satisfaisant la propriété, mais de montrer que tous les graphes connexes avec un sommet de plus que le nombre d’arêtes sont des arbres.
16h04
Ah, d’accord. Donc vous avez raison, ce que vous avez donné est une propriété nécessaire et suffisante si on veut pouvoir supprimer tout aéroport.
Concernant l’ambiguïté du langage, c’est vrai que ce n’est pas forcément clairement défini, mais je n’ai pas souvenir d’avoir été gêné par une telle ambiguïté un jour… Peut-être que l’on peut préciser la chose en disant que, par défaut, « un » donne ∀, mais que si on est dans une possibilité (« on peut »), alors c’est plutôt ∃. Dans le cas général, on dit « pour toute possibilité d’instanciation des variables », mais si on est dans une possibilité, c’est « il existe une instanciation des variables ».
À cela se rajoute peut-être le fait qu’il est aussi naturel de dire « pouvoir fermer tel aéroport (précis) sans perdre la connexité »… Bref.
16h27
Ce que j’ai dit ne fonctionne pas, en fait.
18h57
Dans le problème 9, la phrase « Montrer qu’on peut fermer un aéroport de ce réseau … »
signifie, bien sûr, « Montrer qu’il existe un aéroport de ce réseau tel qu’on puisse fermer cet aéroport … ».
Pour pouvoir fermer TOUT aéroport du réseau sans perdre la possibilité de joindre deux autres quelconques aéroports du réseau, il n’est pas suffisant de supposer que deux quelconques des aéroports sont toujours parcourus par au moins un cycle. Par contre, il est suffisant de supposer, par exemple, que deux quelconques des aéroports sont parcourus par au moins un cycle qui ne passe jamais deux fois par le même aéroport (à l’exception du début et la fin du cycle).
23h34
Proposition de réponse au problème 1 : supposons que nous nous déplaçons de planètes en planètes par les liaisons définies dans l’énoncée. Lorsque j’arrive à destination et je décide de retourner vers mon point de départ, j’emprunterai nécessairement la dernière liaison que j’ai suivi lors de mon arrivée à destination puisqu’elle est unique. D’où l’impossibilité de ne pas passer au moins deux fois par une même liaison.
11h11
Bonjour,
Bravo pour votre proposition de solution au problème 1.
Cependant, elle est incomplète : Que dire du cas où votre planète de départ est la même que celle d’arrivée ?
cordialement,
Sébastien.
21h33
Problème 1
Le tronçon (arête) retour qui mènerait à la planète de départ est nécessairement celui emprunté en premier puisqu’il est unique ( par définition) dans ce cas aussi il est impossible de ne pas emprunter un tronçon deux fois.