Équation des ondes

Des vagues réfractées par un tapis de Sierpinski

Cette simulation montre des vagues, solutions de l’équation des ondes linéaire, interagissant successivement avec six niveaux d’approximation d’un tapis de Sierpinski (ou plutôt de son complémentaire), aussi appelé éponge de Menger de dimension 2. Ce tapis est un fractal, obtenu en subdivisant un carré en neuf carrés plus petits, en enlevant le carré central, puis en répétant cette opération à l’infini pour chacun des carrés plus petits. Dans cette simulation, la vitesse des ondes est réduite d’un facteur \(5/3\) dans les carrés retranchés du tapis. L’état initial est choisi de manière à engendrer une onde circulaire qui se propage et interagit avec le fractal approché. On s’aperçoit que plus le niveau de l’approximation est élevé, plus les vagues sont fragmentées. Cela suggère d’utiliser ce genre de géométrie dans les protections côtières.

Billards isospectraux : on ne peut pas toujours entendre la forme d'un tambour

La question “peut-on entendre la forme d’un tambour” fut popularisée par le mathématicien Mark Kac dans les années 1960. Les vibrations de la membrane d’un tambour sont une superposition de vibrations stationnaires dont les fréquences dépendent de la forme du tambour. Mathématiquement parlant, ces fréquences sont ce qu’on appelle les valeurs propres (ou fréquences propres) de l’opérateur de Laplace, avec conditions aux bords de Dirichlet sur les bords du tambour. L’ensemble de ces valeurs propres s’appelle le spectre du tambour. La question de Mark Kac devient alors la suivante : deux domaines différents peuvent-ils avoir exactement les mêmes fréquences propres de vibration ? Si c’est le cas, alors il existe des tambours différents isospectraux et la réponse à la question est négative. En 1992, Carolyn Gordon, David Webb, et Scott Wolpert furent les premiers à découvrir des tambours isospectraux non équivalents. Cela signifie qu’on ne peut pas transformer un domaine en l’autre par des transformations simples telles que des rotations, des translations ou des réflexions. Les deux domaines sont obtenus en arrangeant de manière différente sept triangles isométriques. La construction marche pour toute déformation des triangles, pour autant que tous leurs angles restent inférieurs à 90 degrés.

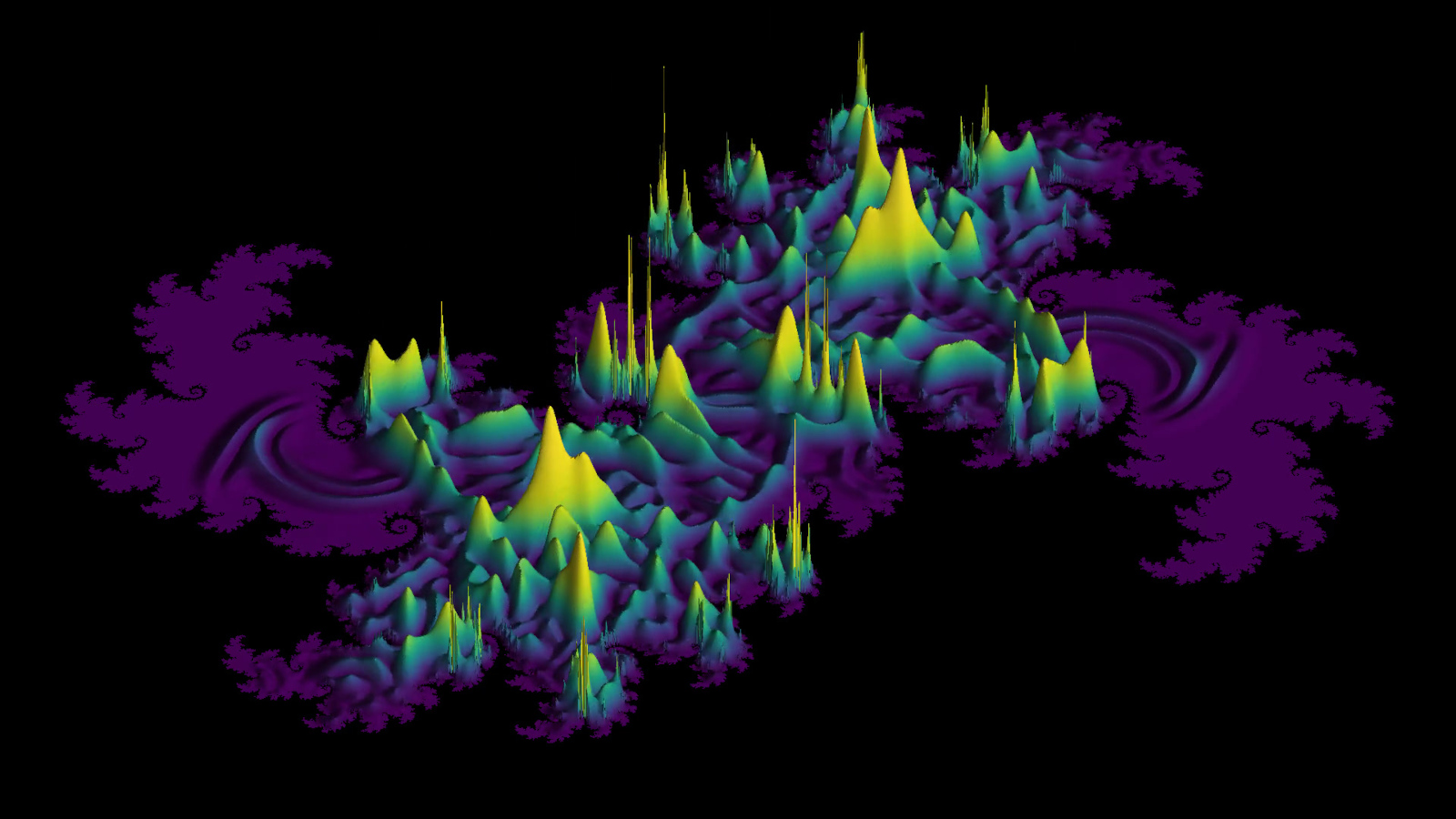
Ondes réfléchies sur l'ensemble de Mandelbrot

Une onde circulaire est réfléchie sur une approximation de l’ensemble de Mandelbrot. La première partie de la simulation montre la hauteur de l’onde, alors que la seconde partie montre sa densité d’énergie. Il n’est pas évident que la réflexion sur un bord fractal, qui n’admet pas de tangente, soit bien définie mathématiquement. Dans cette simulation, toutefois, on n’a pas affaire à un vrai fractal mais à une approximation à bord polygonal de celui-ci. Par conséquent, l’algorithme de simulation est bien défini, même si on n’est pas assuré que la dynamique reste la même si on augmente la résolution. Il semble toutefois que l’onde ne perçoive pas les détails du bord fractal de l’ensemble de Mandelbrot qui sont plus petits que la longueur d’onde. On sait que l’ensemble de Mandelbrot est connexe: on peut relier tous ses points par des chemins ne sortant jamais de l’ensemble. Cette propriété n’est pas respectée par la simulation, qui ignore certains filaments de l’ensemble, trop fins pour la résolution choisie. C’est pourquoi l’onde simulée parvient à franchir ces filaments.

Réflecteurs paraboliques

Cette simulation illustre le fonctionnement de réflecteurs paraboliques, aussi appelés antennes paraboliques. Une onde circulaire est émise au foyer du réflecteur de gauche. Une partie de cette onde ne touche pas ce réflecteur et se propage en se dispersant. Une fraction de cette onde finit par toucher le réflecteur de droite mais elle a perdu en intensité et n’est pas bien focalisée. En revanche, la partie de l’onde réfléchie sur la parabole de gauche est transformée en une onde plane, qui se propage sans perte jusqu’au réflecteur de droite, qui la transforme en une onde circulaire se concentrant au foyer de droite. Ce principe très simple permet de transmettre des ondes sur de très grandes distances, avec très peu de pertes, et de récupérer un signal de bonne qualité. En pratique, le signal émis n’est en général pas une onde circulaire complète, mais seulement une partie d’une telle onde, dirigée uniquement vers le réflecteur de gauche.

Ondes dans une ellipse

La simulation montre la densité d’énergie d’une onde circulaire émise au centre d’une ellipse. L’onde est réfléchie sur le bord de l’ellipse, et au début de la simulation, on observe un front d’onde similaire à celui qu’on obtiendrait en optique géométrique (voir le billet Billards). Toutefois, les fronts d’onde se dégradent peu à peu au cours du temps. Ceci est dû à plusieurs phénomènes qui distinguent l’optique ondulatoire de l’optique géométrique: diffraction, dispersion et interférences. L’optique géométrique, qui suppose que la lumière se propage en ligne droite, est valable dans la limite des longueurs d’onde tendant vers zéro.