Percolation

Percolation sur un processus de disques de Poisson

Cette vidéo montre la percolation dans un cadre un peu moins standard, à savoir sur un processus de disques de Poisson. Les points de ce processus sont disposés de manière aléatoire. Contrairement au processus ponctuel de Poisson, qui est d’une certaine manière le plus aléatoire possible, dans un processus de disques de Poisson on impose une distance minimale entre disques. Les six parties de la simulation font intervenir des réseaux de disques de Poisson de taille de plus en plus grande. Dans chaque partie, chaque disque est ouvert avec une probabilité \(p\), variant de 0 à 1 au cours de la simulation et fermé autrement, indépendamment des autres disques. On considère que les disques communiquent lorsque leur distance est en dessous d’un seuil fixé. Les disques fermés apparaissent en bleu foncé, alors que les disques ouverts apparaissent en jaune s’ils communiquent avec le bord de gauche, et en bleu clair autrement. La composante jaune montre donc la région qu’un liquide peut atteindre, si le bord gauche de l’échantillon est mis en contact avec un réservoir. Une propriété remarquable des modèles de percolation est que la région inondée varie de manière abrupte avec la probabilité \(p\), et ceci d’autant plus que le réseau est grand. Le graphique en haut à droite montre, en fonction de \(p\), le rapport entre le nombre de disques inondés (jaunes) et le nombre de disques ouverts (jaunes ou bleu clairs). Ce rapport augmente abruptement au voisinage de \(0,5\), suggérant que la probabilité critique pour ce modèle de percolation est égale à 1/2.

Taille des amas en percolation de liens sur réseau carré

Cette simulation en six parties illustre la percolation sur les liens de réseaux carrés de taille croissante, qu’on peut voir comme les bords des carrés sur une feuille de papier quadrillé. Dans chaque partie, chaque lien est ouvert avec une probabilité \(p\) et fermé autrement, indépendamment des autres liens. La probabilité \(p\) augmente de 0 à 1 au cours de chaque partie de la simulation. Les liens fermés apparaissent en bleu, alors que les liens ouverts apparaissent en différents niveaux de gris, selon la taille de l’amas ouvert auquel ils appartiennent. Un amas ouvert est un ensemble de liens ouverts qui sont connexes, c’est-à-dire que l’on peut passer d’un lien de l’amas à l’autre en n’empruntant que des liens ouverts. Une propriété remarquable des modèles de percolation est que la distribution des tailles des amas varie de manière abrupte avec la probabilité \(p\), et ceci d’autant plus que le réseau est grand. Pour les liens d’un réseau carré, un amas géant apparaît lorsque \(p\) dépasse la valeur critique \(1/2\). Ce phénomène est illustré par l’histogramme en haut à droite de la vidéo, qui montre la distribution des tailles des amas, sur une échelle logarithmique. Tant que \(p\) est inférieur à \(1/2\), cette distribution est lisse, les amas plus grands étant moins nombreux. Lorsque \(p\) dépasse \(1/2\), la distribution comprend un seul amas géant et un grand nombre d’amas de très petite taille.

Percolation de sites sur réseau triangulaire

Cette simulation en six parties illustre la percolation sur des réseaux triangulaires de taille croissante. Dans chaque partie, chaque triangle équilatéral est ouvert avec une probabilité \(p\) et fermé autrement, indépendamment des autres triangles. La probabilité \(p\) augmente de 0 à 1 au cours de chaque partie de la simulation. Les triangles fermés apparaissent en violet, alors que les triangles ouverts apparaissent soit en jaune, s’ils communiquent avec le bord gauche, soit en rose. La composante jaune montre donc la région qu’un liquide peut atteindre, si le bord gauche de l’échantillon est mis en contact avec un réservoir. Une propriété remarquable des modèles de percolation est que la région inondée varie de manière abrupte avec la probabilité \(p\), et ceci d’autant plus que le réseau est grand. Pour un réseau triangulaire, la probabilité critique à laquelle la transition a lieu, dans la limite des très grandes réseaux, vaut environ \(0,69704\). Le graphique en haut à droite montre, en fonction de \(p\), le rapport entre le nombre de triangles inondés (jaunes) et le nombre de triangles ouverts (jaunes ou roses). Ce rapport augmente abruptement au voisinage de la valeur critique de \(p\).

Percolation de sites sur réseau hexagonal

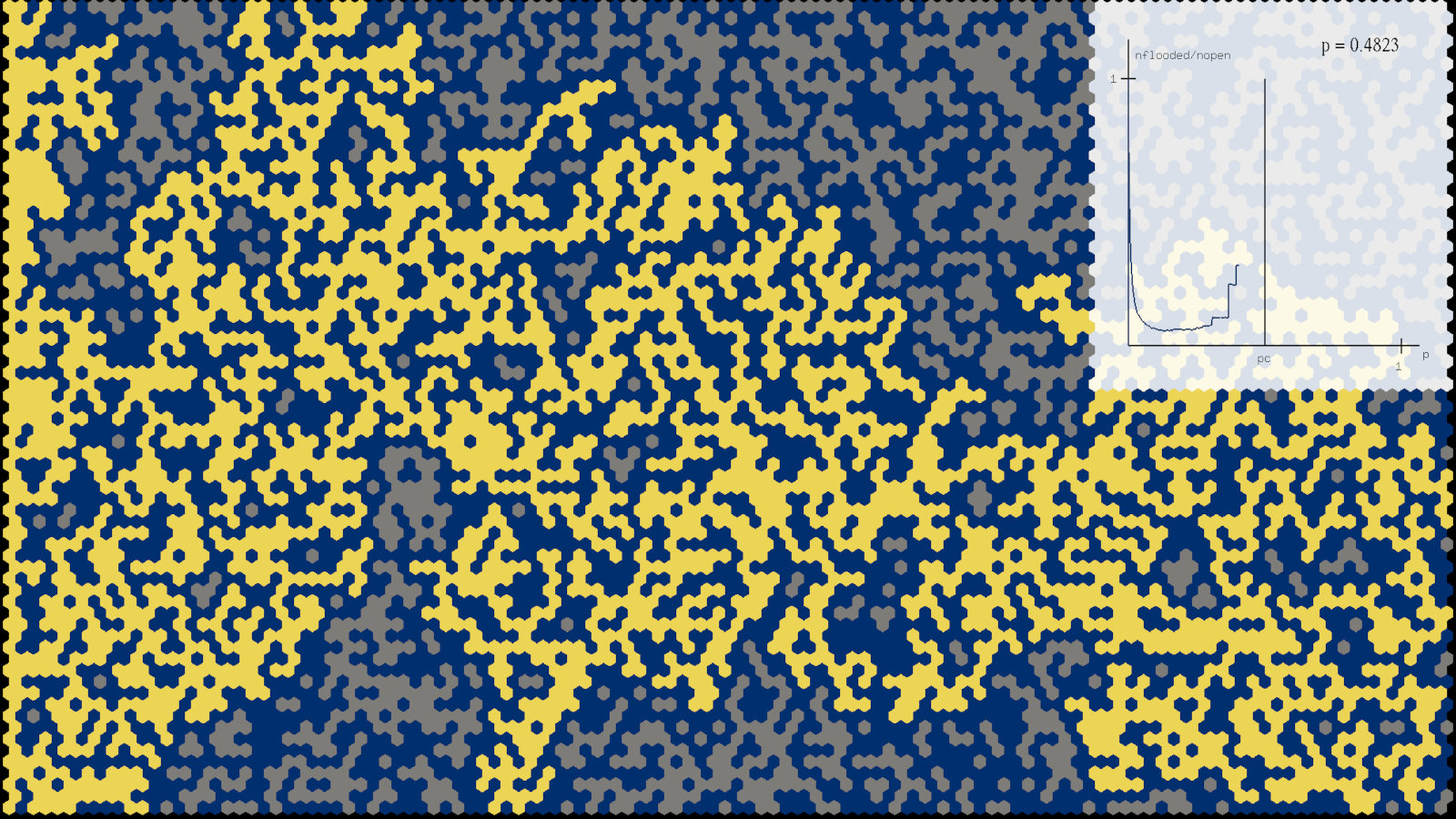
Les modèles de percolation permettent de représenter l’écoulement d’un fluide à travers un milieu poreux. Cette simulation en six parties illustre la percolation sur des réseaux hexagonaux (en nid d’abeille) de taille croissante. Dans chaque partie, chaque hexagone est ouvert avec une probabilité \(p\) et fermé autrement, indépendamment des autres hexagones. La probabilité \(p\) augmente de 0 à 1 au cours de chaque partie de la simulation. Les hexagones fermés apparaissent en bleu, alors que les hexagones ouverts apparaissent soit en jaune, s’ils communiquent avec le bord gauche, soit en gris. La composante jaune montre donc la région qu’un liquide peut atteindre, si le bord gauche de l’échantillon est mis en contact avec un réservoir.

Une propriété remarquable des modèles de percolation est que la région inondée varie de manière abrupte avec la probabilité \(p\), et ceci d’autant plus que le réseau est grand. Pour un réseau hexagonal, on peut montrer que la probabilité critique à laquelle la transition a lieu, dans la limite des très grandes réseaux, est de \(1/2\). Le graphique en haut à droite montre, en fonction de \(p\), le rapport entre le nombre d’hexagones inondés (jaunes) et le nombre d’hexagones ouverts (jaunes ou gris). Ce rapport augmente abruptement au voisinage de la valeur critique \(p=1/2\).